
”¾ĢāÄæ”æČēĶ¼£¬ĖıߊĪ![]() ĪŖÖ±½ĒĢŻŠĪ£¬
ĪŖÖ±½ĒĢŻŠĪ£¬![]() £¬
£¬![]() £¬
£¬![]() £®µć
£®µć![]() “Ó
“Ó![]() ³ö·¢ŅŌĆæĆė2øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņ
³ö·¢ŅŌĆæĆė2øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņ![]() ŌĖ¶Æ£»µć
ŌĖ¶Æ£»µć![]() “Ó
“Ó![]() Ķ¬Ź±³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņ
Ķ¬Ź±³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČĻņ![]() ŌĖ¶Æ£®ĘäÖŠŅ»øö¶Æµćµ½“ļÖÕµćŹ±£¬ĮķŅ»øö¶ÆµćŅ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£®¹żµć
ŌĖ¶Æ£®ĘäÖŠŅ»øö¶Æµćµ½“ļÖÕµćŹ±£¬ĮķŅ»øö¶ÆµćŅ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£®¹żµć![]() ×÷
×÷![]() “¹Ö±
“¹Ö±![]() ÖįÓŚµć
ÖįÓŚµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() ½»
½»![]() ÓŚ
ÓŚ![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £®
£®
(1) Ēó![]() µÄĆ껿
µÄĆ껿![]() ÓėŌĖ¶ÆŹ±¼ä
ÓėŌĖ¶ÆŹ±¼ä![]() µÄŗÆŹż¹ŲĻµŹ½£¬ ²¢Š“³ö×Ō±äĮæ
µÄŗÆŹż¹ŲĻµŹ½£¬ ²¢Š“³ö×Ō±äĮæ![]() µÄȔֵ·¶Ī§£¬ µ±
µÄȔֵ·¶Ī§£¬ µ±![]() ĪŖŗĪÖµŹ±£¬
ĪŖŗĪÖµŹ±£¬![]() µÄÖµ×ī“ó£æ
µÄÖµ×ī“ó£æ
(2)ŹĒ·ń“ęŌŚµć![]() £¬Ź¹µĆ
£¬Ź¹µĆ![]() ĪŖÖ±½ĒČż½ĒŠĪ?Čō“ęŌŚ£¬Ēó³öµć
ĪŖÖ±½ĒČż½ĒŠĪ?Čō“ęŌŚ£¬Ēó³öµć![]() µÄ×ų±ź£¬Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
µÄ×ų±ź£¬Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
(3) µ±![]() ĪŖŅŌ
ĪŖŅŌ![]() ĪŖµ×µÄµČŃüČż½ĒŠĪŹ±£¬Ēó
ĪŖµ×µÄµČŃüČż½ĒŠĪŹ±£¬Ēó![]() Öµ£®
Öµ£®
(4) ŹĒ·ń“ęŌŚÕāŃłµÄ![]() Öµ£¬Ź¹Ö±Ļß
Öµ£¬Ź¹Ö±Ļß![]() ½«
½«![]() µÄÖܳ¤ŗĶĆ껿Ķ¬Ź±Ę½·Ö?Čō“ęŌŚ£¬Ēó³ö
µÄÖܳ¤ŗĶĆ껿Ķ¬Ź±Ę½·Ö?Čō“ęŌŚ£¬Ēó³ö![]() Öµ£¬Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
Öµ£¬Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©![]() £¬µ±
£¬µ±![]() Ź±£¬ÓŠ
Ź±£¬ÓŠ![]() £»£Ø2£©
£»£Ø2£©![]() »ņ
»ņ![]() £»£Ø3£©
£»£Ø3£©![]() £»£Ø4£©“ęŌŚ£¬µ±
£»£Ø4£©“ęŌŚ£¬µ±![]() Ź±£¬Ö±Ļß
Ź±£¬Ö±Ļß![]() ½«
½«![]() µÄÖܳ¤ŗĶĆ껿Ķ¬Ź±Ę½·Ö.
µÄÖܳ¤ŗĶĆ껿Ķ¬Ź±Ę½·Ö.
”¾½āĪö”æ
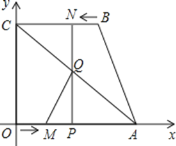
£Ø1£©¹żµćB×÷BD”ĶxÖįÓŚD£¬øł¾Ż¾ŲŠĪµÄŠŌÖŹæɵĆBN=PD=t£¬OD=BC=3£¬Č»ŗóøł¾ŻµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹæɵĆ![]() ,øł¾ŻČż½ĒŠĪĆ껿¹«Ź½¼“æÉĒó³ö
,øł¾ŻČż½ĒŠĪĆ껿¹«Ź½¼“æÉĒó³ö![]() µÄĆ껿
µÄĆ껿![]() ÓėŌĖ¶ÆŹ±¼ä
ÓėŌĖ¶ÆŹ±¼ä![]() µÄŗÆŹż¹ŲĻµŹ½£¬Č»ŗóøł¾ŻĢāŅā¼“æÉĒó³ötµÄȔֵ·¶Ī§£¬ŌŁĄūÓƶž“ĪŗÆŹżĒó×īÖµ¼“æÉ£»
µÄŗÆŹż¹ŲĻµŹ½£¬Č»ŗóøł¾ŻĢāŅā¼“æÉĒó³ötµÄȔֵ·¶Ī§£¬ŌŁĄūÓƶž“ĪŗÆŹżĒó×īÖµ¼“æÉ£»
£Ø2£©øł¾ŻÖ±½ĒµÄĒéæö·ÖĄąĢÖĀŪ£¬·Ö±šÕŅ³öµČĮæ¹ŲĻµĮŠ³ö·½³Ģ£¬¼“æÉĒó³ötµÄÖµ£»
£Ø3£©·Ö±šÓĆŗ¬tµÄŹ½×Ó±ķŹ¾³öAQŗĶAM£¬Č»ŗóøł¾ŻµČŃüČż½ĒŠĪµÄ¶ØŅåĮŠ·½³Ģ£¬¼“æÉĒó³ötµÄÖµ£»
£Ø4£©·Ö±šĒó³öÖ±Ļß![]() ½«
½«![]() µÄÖܳ¤Ę½·ÖµÄtÖµŗĶÖ±Ļß
µÄÖܳ¤Ę½·ÖµÄtÖµŗĶÖ±Ļß![]() ½«
½«![]() µÄĆę»żĘ½·ÖµÄtÖµ£¬Čē¹ūĮ½øötÖµĻąµČ¼““ęŌŚ£¬²»ĻąµČ¼“²»“ęŌŚ£®
µÄĆę»żĘ½·ÖµÄtÖµ£¬Čē¹ūĮ½øötÖµĻąµČ¼““ęŌŚ£¬²»ĻąµČ¼“²»“ęŌŚ£®
½ā£ŗ£Ø1£©¹żµćB×÷BD”ĶxÖįÓŚD
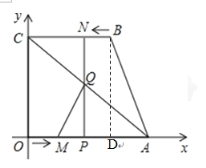
Ņ×ÖŖ£ŗĖıߊĪCOPN”¢ĖıߊĪNPDBŗĶĖıߊĪCODB¾łĪŖ¾ŲŠĪ
”ąBN=PD=t£¬OD=BC=3
![]()
”ąAD=OA£OD=1![]()
![]()
![]()
![]()
µćM“ÓµćOµ½µćAĖłŠčŹ±¼äĪŖ£ŗOA”Ā2=2s£¬µćN“ÓµćBµ½µćCĖłŠčŹ±¼äĪŖ£ŗBC”Ā1=3s£¬
”ą![]()
»ÆĪŖ¶„µćŹ½£¬µĆ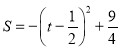 £¬ĘäÖŠ-1£¼0
£¬ĘäÖŠ-1£¼0
”ąµ±![]() Ź±£¬ÓŠ
Ź±£¬ÓŠ![]()
£Ø2£©¢Łµ±![]() Ź±£¬
Ź±£¬
![]()
”ą”÷AQMĪŖµČŃüÖ±½ĒČż½ĒŠĪ
”ßQP”ĶAM
”ąQPĪŖ”÷AQMµÄÖŠĻß
![]()
![]()
½āµĆ£ŗ![]()
¢Ś![]() Ź±£¬“ĖŹ±MÓėPÖŲŗĻ
Ź±£¬“ĖŹ±MÓėPÖŲŗĻ
”ą![]()
![]()
½āµĆ![]()
×ŪÉĻ£¬![]() »ņ
»ņ![]()
£Ø3£©”ß![]() ĪŖŅŌ
ĪŖŅŌ![]() ĪŖµ×µÄµČŃüČż½ĒŠĪ
ĪŖµ×µÄµČŃüČż½ĒŠĪ
![]()
ŌŚRt”÷AQPÖŠ![]()
ӧ![]()
”ą![]()
½āµĆ£ŗ![]()
£Ø4£©Ćę»żĘ½·ÖŹ±£¬¼“S”÷APQ=![]() S”÷AOC
S”÷AOC
![]()
¼“![]()
½āµĆ£ŗ![]() »ņ
»ņ![]() £Ø²»·ūŗĻŹµ¼Ź£¬¹ŹÉįČ„£©
£Ø²»·ūŗĻŹµ¼Ź£¬¹ŹÉįČ„£©
Öܳ¤Ę½·ÖŹ±£ŗ![]() £®
£®
¼“![]()
½āµĆ![]()
×ŪÉĻĖłŹö£ŗµ±![]() Ź±£¬Ö±Ļß
Ź±£¬Ö±Ļß![]() ½«
½«![]() µÄÖܳ¤ŗĶĆ껿Ķ¬Ź±Ę½·Ö£®
µÄÖܳ¤ŗĶĆ껿Ķ¬Ź±Ę½·Ö£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬¶ž“ĪŗÆŹżµÄĶ¼Ļó¾¹ż![]() £¬
£¬![]() £¬
£¬![]() Čżµć£®
Čżµć£®
£Ø1£©Ēóøƶž“ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©µć![]() ŹĒĻ߶Ī
ŹĒĻ߶Ī![]() ÉĻµÄ¶Æµć£Øµć
ÉĻµÄ¶Æµć£Øµć![]() ÓėĻ߶Ī
ÓėĻ߶Ī![]() µÄ¶Ėµć²»ÖŲŗĻ£©£¬Čō
µÄ¶Ėµć²»ÖŲŗĻ£©£¬Čō![]() Óė
Óė![]() ĻąĖĘ£¬Ēóµć
ĻąĖĘ£¬Ēóµć![]() µÄ×ų±ź£®
µÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ”÷ABCŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠµÄĪ»ÖĆČēĶ¼ĖłŹ¾£®

£Ø1£©»³ö”÷ABCČʵćC°“Ė³Ź±Õė·½ĻņŠż×Ŗ90”ćµÄ”÷A”äB”äC£¬²¢Ö±½ÓŠ“³öµćAŌŚŠż×Ŗ¹ż³ĢÖŠĖł¾¹żµÄĀ·¾¶³¤£Ø½į¹ū±£Įō![]() £©£»
£©£»
£Ø2£©ŌŚ£Ø1£©µÄĢõ¼žĻĀ£¬ĄūÓĆ³ß¹ę×÷Ķ¼»³ö”÷A”äB”äCµÄĶā½ÓŌ²”ŃP£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼×”¢ŅŅĮ½ČĖ½ųŠŠĆžÅĘÓĪĻ·ĻÖÓŠČżÕųżŹż×ÖĶā¶¼ĻąĶ¬µÄÅĘ£¬ÕżĆę·Ö±š±źÓŠŹż×Ö2£¬5£¬6£®½«ČżÕÅÅʱ³Ćę³ÆÉĻ£¬Ļ“ŌČŗó·ÅŌŚ×Ą×ÓÉĻ£®
£Ø1£©¼×“ÓÖŠĖ껜³éČ”Ņ»ÕÅÅĘ£¬¼ĒĀ¼Źż×Öŗó·Å»ŲĻ“ŌČ£¬ŅŅŌŁĖ껜³éČ”Ņ»ÕÅĒėÓĆĮŠ±ķ·Ø»ņ»Ź÷דĶ¼µÄ·½·Ø£¬ĒóĮ½ČĖ³éČ”ĻąĶ¬Źż×ÖµÄøÅĀŹ£»
£Ø2£©ČōĮ½ČĖ³éČ”µÄŹż×ÖŗĶĪŖ4µÄ±¶Źż£¬Ōņ¼×»ńŹ¤£»Čō³éČ”µÄŹż×ÖŗĶĪŖĘꏿ£¬ŌņŅŅ»ńŹ¤ÕāÓĪĻ·¹«Ę½Āš£æĒėÓĆøÅĀŹµÄÖŖŹ¶¼ÓŅŌ½āŹĶ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĮĖ½āÉīŪŚŹŠ³õ֊ѧɜæĪĶāŌĶĮĒéæö£¬µ÷²éŠ”×é¶ŌøĆŹŠÕāѧʌ³õ֊ѧɜŌĶĮæĪĶāŹé¼®µÄ²įŹż½ųŠŠĮĖ³éŃłµ÷²é£¬²¢øł¾Żµ÷²é½į¹ū»ęÖĘ³ÉČēĻĀĶ³¼ĘĶ¼£®
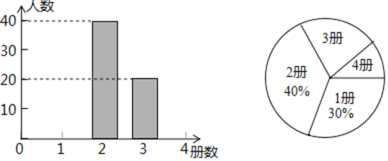
øł¾ŻĶ³¼ĘĶ¼Ģį¹©µÄŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©±¾“Ī³éŃłµ÷²éµÄŃł±¾ČŻĮæŹĒ £»
£Ø2£©²¹Č«ĢõŠĪĶ³¼ĘĶ¼£»
£Ø3£©øĆŹŠ¹²ÓŠ218000Ćū³õÖŠÉś£¬¹Ą¼ĘøĆŹŠ³õ֊ѧɜÕāѧʌæĪĶāŌĶĮ³¬¹ż2²įµÄČĖŹż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÖĘ×÷ijÖÖ½šŹō¹¤¾ßŅŖ½ųŠŠ²ÄĮĻģŃÉÕŗĶ¶ĶŌģĮ½øö¹¤Šņ£¬¼“ŠčŅŖ½«²ÄĮĻÉÕµ½800 ”ę£¬Č»ŗóĶ£Ö¹ģŃÉÕ½ųŠŠ¶ĶŌģ²Ł×÷£¬¾¹ż8minŹ±£¬²ÄĮĻĪĀ¶Č½µĪŖ600”ę£¬ģŃÉÕŹ±ĪĀ¶Čy(”ę)ÓėŹ±¼äx(min)³ÉŅ»“ĪŗÆŹż¹ŲĻµ£»¶ĶŌģŹ±£¬ĪĀ¶Čy(”ę)ÓėŹ±¼äx(min)³É·“±ČĄżŗÆŹż¹ŲĻµ(ČēĶ¼)£¬ŅŃÖŖøĆ²ÄĮĻ³õŹ¼ĪĀ¶ČŹĒ26 ”ę£®
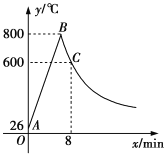
£Ø1£©·Ö±šĒó³ö²ÄĮĻģŃÉÕŗĶ¶ĶŌģŹ±y¹ŲÓŚxµÄŗÆŹż½āĪöŹ½£¬²¢Š“³ö×Ō±äĮæxµÄȔֵ·¶Ī§£»
£Ø2£©øł¾Ż¹¤ŅÕŅŖĒ󣬵±²ÄĮĻĪĀ¶ČµĶÓŚ400”ꏱ£¬ŠėĶ£Ö¹²Ł×÷£¬ÄĒĆ“¶ĶŌģµÄ²Ł×÷Ź±¼äÓŠ¶ą³¤£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
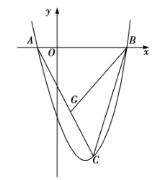
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÅ×ĪļĻßy£½ax2+bx+c£Øa”Ł0£©µÄ¶Ō³ĘÖįĪŖÖ±Ļßx£½©1£¬ĒŅÅ×ĪļĻß¾¹żA£Ø1£¬0£©£¬C£Ø0£¬3£©Į½µć£¬ÓėxÖį½»ÓŚµćB£®

£Ø1£©ČōÖ±Ļßy£½mx+n¾¹żB”¢CĮ½µć£¬ĒóÖ±ĻßBCŗĶÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©ŌŚÅ×ĪļĻߵĶŌ³ĘÖįx£½©1ÉĻÕŅŅ»µćM£¬Ź¹µćMµ½µćAµÄ¾ąĄėÓėµ½µćCµÄ¾ąĄėÖ®ŗĶ×īŠ”£¬Ēó³öµćMµÄ×ų±ź£ŗ
£Ø3£©ŌŚÅ×ĪļĻßÉĻ“ęŌŚµćP(²»ÓėCÖŲŗĻ)£¬Ź¹µĆ”÷APBµÄĆ껿Óė”÷ACBµÄĆ껿ĻąµČ£¬ĒóµćPµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ±ķÖŠĖłĮŠ ![]() µÄ7¶ŌÖµŹĒ¶ž“ĪŗÆŹż
µÄ7¶ŌÖµŹĒ¶ž“ĪŗÆŹż![]() Ķ¼ĻóÉĻµÄµćĖł¶ŌÓ¦µÄ×ų±ź£¬ĘäÖŠ
Ķ¼ĻóÉĻµÄµćĖł¶ŌÓ¦µÄ×ų±ź£¬ĘäÖŠ ![]()
x | ” |
|
|
|
|
|
|
| ” |
y | ” | 7 | m | 14 | k | 14 | m | 7 | ” |
øł¾Ż±ķÖŠĢį¹©µÄŠÅĻ¢£¬ÓŠŅŌĻĀ4 øöÅŠ¶Ļ£ŗ
¢Ł ![]() £»¢Ś
£»¢Ś ![]() £»¢Ū µ±
£»¢Ū µ±![]() Ź±£¬y µÄÖµŹĒ k£»¢Ü
Ź±£¬y µÄÖµŹĒ k£»¢Ü ![]() ĘäÖŠÅŠ¶ĻÕżČ·µÄŹĒ £Ø £©
ĘäÖŠÅŠ¶ĻÕżČ·µÄŹĒ £Ø £©
A. ¢Ł¢Ś¢Ū B. ¢Ł¢Ś¢Ü C. ¢Ł¢Ū¢Ü D. ¢Ś¢Ū¢Ü
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÅ×ĪļĻßy=ax2+bx+cµÄ¶Ō³ĘÖįĪŖÖ±Ļßx=©1£¬²æ·ÖĶ¼ĻóČēĶ¼ĖłŹ¾£¬ĻĀĮŠÅŠ¶ĻÖŠ£ŗ
¢Łabc£¾0£»
¢Śb2©4ac£¾0£»
¢Ū9a©3b+c=0£»
¢ÜČōµć£Ø©0.5£¬y1£©£¬£Ø©2£¬y2£©¾łŌŚÅ×ĪļĻßÉĻ£¬Ōņy1£¾y2£»
¢Ż5a©2b+c£¼0£®
ĘäÖŠÕżČ·µÄøöŹżÓŠ£Ø””””£©
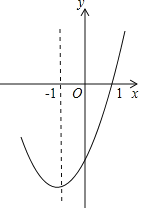
A. 2 B. 3 C. 4 D. 5
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com