
 如图,已知A是定角∠MON的平分线上的一个定点,过A任作一条直线与OM、ON分别交于P、Q,求证:$\frac{1}{OP}$+$\frac{1}{OQ}$为定值.
如图,已知A是定角∠MON的平分线上的一个定点,过A任作一条直线与OM、ON分别交于P、Q,求证:$\frac{1}{OP}$+$\frac{1}{OQ}$为定值. 分析 过Q作QB∥AO,交PO的延长线于B,作OC⊥BQ于C,由平行线的性质得到∠AOP=∠B,∠AOQ=∠BQO,根据角平分线的定义得到∠AOP=∠AOQ=$\frac{1}{2}$∠MON,证得OQ=OB,求得OQ+OP=OB+OP=PB,根据分式的运算得到$\frac{1}{OP}+\frac{1}{OQ}=\frac{OP+OB}{OP•OQ}=\frac{PB}{OP•OQ}$,①根据线段垂直平分线的定义证得CQ=$\frac{1}{2}$BQ,根据QB∥AO,推出$\frac{PB}{OP}=\frac{BQ}{OA}$②,把②代入①通过化简即可得到结论.
解答 证明:过Q作QB∥AO,交PO的延长线于B,作OC⊥BQ于C,
∴∠AOP=∠B,∠AOQ=∠BQO,
∵OA平分∠MON,
∴∠AOP=∠AOQ=$\frac{1}{2}$∠MON,
∴OQ=OB,
∴OQ+OP=OB+OP=PB,
∴$\frac{1}{OP}+\frac{1}{OQ}=\frac{OP+OB}{OP•OQ}=\frac{PB}{OP•OQ}$,①
∵OQ=OB,OC⊥BQ,
∴CQ=$\frac{1}{2}$BQ,
∵QB∥AO,
∴$\frac{PB}{OP}=\frac{BQ}{OA}$②,
把②代入①得:$\frac{1}{OP}$+$\frac{1}{OQ}$=$\frac{BQ}{OA•OQ}=\frac{2}{OA}×\frac{\frac{BQ}{2}}{OQ}$=$\frac{2}{OA}$×$\frac{CQ}{OQ}$=$\frac{2}{OA}$•cos$∠BQO=\frac{2}{OA}×cos\frac{1}{2}∠MON$③,
∵OA是一个定值,∠MON是一个定值,
∴③式是一个定值,
∴$\frac{1}{OP}$+$\frac{1}{OQ}$为定值.
点评 本题考查了相似三角形的判定和性质,平行线的性质,角平分线的定义,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD中,AB=30,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G.连接AG、CF.下列结论:①△ABG≌△AFG;②BG=15;③△CFG是正三角形;④△FGC的面积为90.其中正确的是①②④(填所有正确答案的序号).
如图,正方形ABCD中,AB=30,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G.连接AG、CF.下列结论:①△ABG≌△AFG;②BG=15;③△CFG是正三角形;④△FGC的面积为90.其中正确的是①②④(填所有正确答案的序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AB=AC,D为△ABC外一点,且∠BDC=∠BAC,BD交AC于O,AM⊥BD于M
如图,△ABC中,AB=AC,D为△ABC外一点,且∠BDC=∠BAC,BD交AC于O,AM⊥BD于M 查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.5×108 | B. | 2.5×109 | C. | 2.5×1010 | D. | 2.5×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,方格图中小正方形的边长为1.将方格图中阴影部分图形剪下来,再把剪下的阴影部分重新剪拼成一个正方形,那么所拼成的这个正方形的边长等于( )
如图,方格图中小正方形的边长为1.将方格图中阴影部分图形剪下来,再把剪下的阴影部分重新剪拼成一个正方形,那么所拼成的这个正方形的边长等于( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
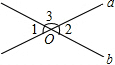 如图,直线a,b相交于点O,若∠1=50°,则∠2和∠3的度数分别是( )
如图,直线a,b相交于点O,若∠1=50°,则∠2和∠3的度数分别是( )| A. | 50°,40° | B. | 50°,130° | C. | 130°,50° | D. | 50°,50° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com