
 某服装店专营一批进价为每件200元的品牌衬衫,每件售价为300元,每天可售出40件,若每件降价10元,则每天多售出10件,请根据以上信息解答下列问题:
某服装店专营一批进价为每件200元的品牌衬衫,每件售价为300元,每天可售出40件,若每件降价10元,则每天多售出10件,请根据以上信息解答下列问题:分析 (1)表示出每件商品的利润和销量进而得出等式求出答案;
(2)分别表示出100件商品的利润进而得出等式求出答案.
解答 解:(1)设该品牌衬衫每件售价为x元,根据题意可得:
(x-200)(40+$\frac{300-x}{10}$×10)=4500,
解得:x1=250,x2=290,
因为要让利于顾客,所以应采取降价销售且降得越多越好,
故x=250,
答:该品牌衬衫每件售价为250元;
(2)根据题意可得:250×80+250×80%×(100-80)=(200-a)×100(1+50%),
解得:a=40,
答:a的值为40.
点评 此题主要考查了一元二次方程的应用,正确表示出商品总利润是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
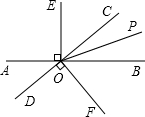 如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD
如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD查看答案和解析>>
科目:初中数学 来源: 题型:解答题
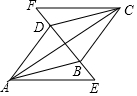 如图,将四边形ABCD的对角线BD向两个方向延长,分别至点E和点F,且使BE=DF,若AE∥CF且AE=CF.
如图,将四边形ABCD的对角线BD向两个方向延长,分别至点E和点F,且使BE=DF,若AE∥CF且AE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 项目 | 跳绳 | 踢毽子 | 乒乓球 | 羽毛球 | 其他 |
| 人数(人) | 14 | 10 | 8 | 6 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC是直角三角形,∠C=90°.
如图,△ABC是直角三角形,∠C=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com