
分析 先根据二次函数的性质得到抛物线的对称轴为直线x=2,再根据抛物线与x轴的交点(对称轴左侧)落在0和2之间(不与0和2重合),则可判断抛物线与y轴的交点在x轴上方,即2-m>0,于是可求出m=1,然后判断点(m-2,5-m)落在的象限.
解答 解:抛物线的对称轴为直线x=-$\frac{-4m}{2m}$=2,
∵抛物线与x轴的交点(对称轴左侧)落在0和2之间(不与0和2重合),
∴2-m>0,解得m<2,
∵m为正整数,
∴m=1,
∴点(m-2,5-m),即(-1,4)落在第二象限.
故答案为二.
点评 本题考查了抛物线与x轴的交点:二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系,△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点P为∠AOB内部一点,PD⊥OA于点D,PB⊥OB于点C,请补充一条件,使点P一定在△AOB的平分线上.你补充的条件是:PD=PC.
如图,点P为∠AOB内部一点,PD⊥OA于点D,PB⊥OB于点C,请补充一条件,使点P一定在△AOB的平分线上.你补充的条件是:PD=PC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
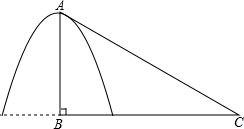 如图,从帐篷支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷,若绳子的长度为5.5米,固定点C到帐篷支撑杆底部B的距离是4.5米,现有一根高为3.2米的竿,它能否做帐篷的支撑竿,请说明理由.
如图,从帐篷支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷,若绳子的长度为5.5米,固定点C到帐篷支撑杆底部B的距离是4.5米,现有一根高为3.2米的竿,它能否做帐篷的支撑竿,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com