
【题目】设![]() 是
是![]() 的平均数,即
的平均数,即![]() ,则方差
,则方差![]() ,它反映了这组数的波动性,
,它反映了这组数的波动性,
(1)证明:对任意实数a,x1a,x2a,…,xna,与x1,x2,…,xn 方差相同;
(2)证明![]() ;
;
(3)以下是我校初三(1)班 10 位同学的身高(单位:厘米):
169,172,163,173,175,168,170,167,170,171,计算这组数的方差.
科目:初中数学 来源: 题型:
【题目】已如如图1,在平面直角坐标系中,点A的坐标为(6,0)、点B的坐标为(0,8),点C在y轴上,作直线AC.点B关于直线AC的对称点B′刚好在x轴上,连接CB′.
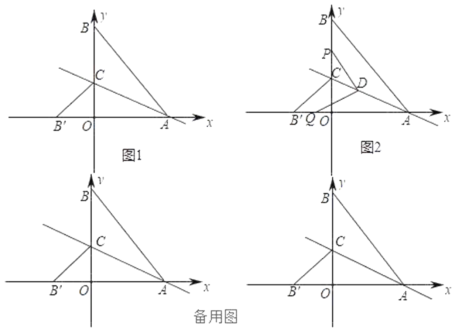
(1)写出点B′的坐标,并求出直线AC对应的函数表达式;
(2)点D在线段AC上,连接DB、DB′、BB′,当△DBB′是等腰直角三角形时,求点D坐标;
(3)如图2,在(2)的条件下,点P从点B出发以每秒2个单位长度的速度向原点O运动,到达点O时停止运动,连接PD,过D作DP的垂线,交x轴于点Q,问点P运动几秒时△ADQ是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七、八年级各有10名同学参加市级数学竞赛,各参赛选手的成绩如下(单位:分):
七年级:89,92,92,92,93,95,95,96,98,98
八年级:88,93,93,93,94,94,95,95,97,98
整理得到如下统计表
年级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
七年级 | 98 | 94 | a | m | 7.6 |
八年级 | 98 | n | 94 | 93 | 6.6 |
根据以上信息,完成下列问题
(1)填空:a= ;m= ;n= ;
(2)两个年级中, 年级成绩更稳定;
(3)七年级两名最高分选手分别记为:A1,A2,八年级第一、第二名选手分别记为B1,B2,现从这四人中,任意选取两人参加市级经验交流,请用树状图法或列表法求出这两人分别来自不同年级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点P为BC的中点,连接EP,AD.
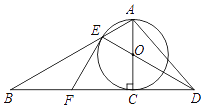
(1)求证:PE是⊙O的切线;
(2)若⊙O的半径为3,∠B=30°,求P点到直线AD的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
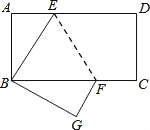
【题目】如图,长方形ABCD中AD∥BC,边AB=4,BC=8.将此长方形沿EF折叠,使点D与点B重合,点C落在点G处.
(1)试判断△BEF的形状,并说明理由;
(2)求△BEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
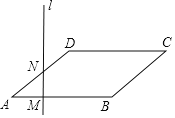
【题目】如图,点![]() 为平行四边形
为平行四边形![]() 的边
的边![]() 上一动点,过点
上一动点,过点![]() 作直线
作直线![]() 垂直于
垂直于![]() ,且直线
,且直线![]() 与平行四边形
与平行四边形![]() 的另一边交于点
的另一边交于点![]() .当点
.当点![]() 从
从![]() 匀速运动时,设点
匀速运动时,设点![]() 的运动时间为
的运动时间为![]() ,
,![]() 的面积为
的面积为![]() ,能大致反映
,能大致反映![]() 与
与![]() 函数关系的图象是( )
函数关系的图象是( )
A.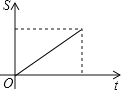 B.
B.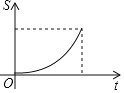
C.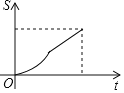 D.
D.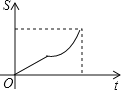
查看答案和解析>>
科目:初中数学 来源: 题型:
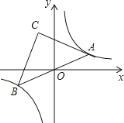
【题目】如图,点A是双曲线![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
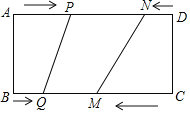
【题目】如图,在矩形ABCD中,BC=20cm,P、Q、M、N分别从A、B、C、D出发沿AD、BC、CB、DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时即停止.已知在相同时间内,若BQ=xcm(x≠0),则AP=2xcm,CM=3xcm,DN=x2cm.
(Ⅰ)当x为何值时,AP、ND长度相等?
(Ⅱ)当x为何值时,以PQ、MN为两边,以矩形的边(AD或BC)的一部分为第三边能构成一个三角形?
(Ⅲ)当x为何值时,以P、Q、M、N为顶点的四边形是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() (a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.
(a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.

(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为等腰三角形,请直接写出所有符合条件的点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com