解:(1)PG⊥PC,PG=PC.
理由如下:如图1,延长GP交CD于H,
∵P是线段DF的中点,
∴DP=FP,
∵正方形ABCD和正方形BEFG的点A、B、E在同一条直线上,
∴DC∥AE∥GF,
∴∠PDH=∠PFG,∠PHD=∠PGF,
∵在△PDH和△PFG中,
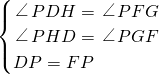
∴△PDH≌△PFG(AAS),
∴PH=PG,DH=FG,
∵CH=CD-DH,CG=BC-BG,BC=CD,
∴CH=CG,
∴△CHG是等腰直角三角形,
∴PG⊥PC,PG=PC;
(2)①如图,延长GP交CD于H,与(1)同理可得PH=PG,CH=CG,
∴△CGH是等腰三角形,
∵∠ABC=∠BEF=60°,
∴∠BCD=120°,
∴∠CGP=

(180°-120°)=30°,
又∵PH=PG,
∴PG⊥PC,
PC=PG•tan∠CGP=PG•tan30°=

PG,
故,PG⊥PC,PC=

PG;
②∵∠ABC=∠BEF=2α,
∴∠BCD=180°-2α,
∵△CGH是等腰三角形,
∴∠CGP=

[180°-(180°-2α)]=α,
又∵PH=PG,
∴PG⊥PC,
PC=PG•tan∠CGP=PG•tanα,
故PG⊥PC,PC=PG•tanα.
分析:(1)延长GP交CD于H,根据中点的定义可得DP=FP,根据两直线平行,内错角相等可得∠PDH=∠PFG,∠PHD=∠PGF,然后利用“角角边”证明△PDH和△PFG全等,根据全等三角形的可得PH=PG,DH=FG,然后求出CH=CG,再根据等腰直角三角形的性质解答;
(2)①延长GP交CD于H,与(1)同理求出PH=PG,CH=CG,然后求出△CGH是等腰三角形,然后根据菱形的邻角互补求出∠BCD=120°,再根据等腰三角形的两底角相等求出∠CGP=30°,根据等腰三角形三线合一可得PG⊥PC,再解直角三角形即可得到PC=

PG;
②根据菱形的邻角互补求出∠BCD=180°-2a,与①同理求出△CGH是等腰三角形,然后根据等腰三角形两底角相等求出∠CGP=α,根据等腰三角形三线合一的性质可得PG⊥PC,再解直角三角形即可得到PC=PGtanα.
点评:本题考查了正方形的性质,全等三角形的判定与性质,等腰三角形两底角相等,等腰三角形三线合一的性质,以及菱形的性质,熟练掌握各图形的性质并作辅助线构造出全等三角形是解题的关键,每一小题的求解思路基本相同是此类题目的最大特点.


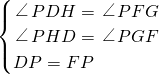

 (180°-120°)=30°,
(180°-120°)=30°, PG,
PG, PG;
PG; [180°-(180°-2α)]=α,
[180°-(180°-2α)]=α, PG;
PG;

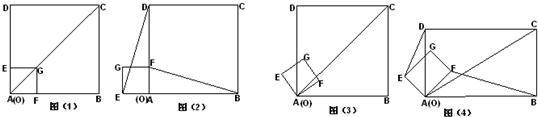
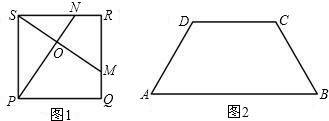 构造一个与上述命题类似的正确命题并加以证明.
构造一个与上述命题类似的正确命题并加以证明.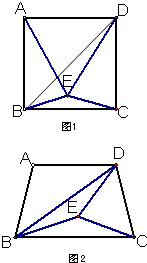 26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.
26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.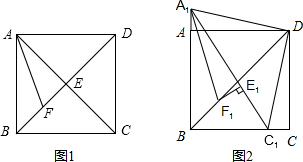 如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.
如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.