
【题目】A、B两地相距64 km,甲从A地出发,每小时行14 km,乙从B地出发,每小时行18 km.
(1)若两人同时出发相向而行,则需经过几小时两人相遇?
(2)若两人同时出发相向而行,则需经过几小时两人相距16 km?
(3)若甲在前,乙在后,两人同时同向而行,则几小时后乙超过甲10 km?
【答案】(1) 2小时;(2) 1.5小时或2.5小时;(3) 18.5小时.
【解析】
(1)如果两人同时出发相向而行,那么是相遇问题,设两人同时出发相向而行,需经过x小时两人相遇,即x小时他们共同走完64千米,由此可以列出方程解决问题;
(2) 此小题有两种情况:①还没有相遇他们相距16千米;②已经相遇他们相距16千米.但都可以利用相遇问题解决;
(3) 若甲在前,乙在后,两人同时同向而行,此时是追及问题,设![]() 小时后乙超过甲10千米,那么
小时后乙超过甲10千米,那么![]() 小时甲走了14
小时甲走了14![]() 千米,乙走了18
千米,乙走了18![]() 千米,然后利用已知条件即可列出方程解决问题.
千米,然后利用已知条件即可列出方程解决问题.
解:(1)设两人同时出发相向而行,需经过x小时两人相遇,
![]()
![]()
答:两人同时出发相向而行,需经过2小时两人相遇;
(2)设两人同时出发相向而行,需y小时两人相距16千米,
①当两人没有相遇他们相距16千米,
![]()
![]()
②当两人已经相遇他们相距16千米,
![]()
![]()
答:若两人同时出发相向而行,则需1.5或2.5小时两人相距16千米;
(3)设甲在前,乙在后,两人同时同向而行,则z小时后乙超过甲10千米,
![]()
![]()
答:若甲在前,乙在后,两人同时同向而行,则18.5小时后乙超过甲10千米.
故答案是:(1) 2小时;(2) 1.5小时或2.5小时;(3) 18.5小时.


科目:初中数学 来源: 题型:
【题目】在平行四边形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() .要使四边形
.要使四边形![]() 是正方形,还需添加一组条件.下面给出了五组条件:①
是正方形,还需添加一组条件.下面给出了五组条件:①![]() ,且
,且![]() ;②
;②![]() , 且
, 且![]() ;③
;③![]() ,且
,且![]() ;④
;④![]() ,且
,且![]() ;⑤
;⑤![]() ,且
,且![]() .其中正确的是________(填写序号).
.其中正确的是________(填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为给人们的生活带来方便,2017年兴化市准备在部分城区实施公共自行车免费服务.图1是公共自行车的实物图,图2是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=35cm,DF=24cm,AF=30cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°. (参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)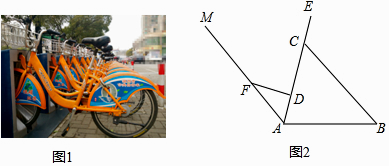
(1)求AD的长;
(2)求点E到AB的距离(结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验室里,水平桌面上有甲、乙、丙三个相 同高度的圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在10cm高度处连通(即管子底部离容器底10cm),现三个容器中,只有乙中有水,水位高4cm,如图所示.若每分钟同时向甲和丙注入相同量的水,开始注水1分钟,甲的水位上升3cm.则开始注入 分钟水量后,甲的水位比乙高1cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图A、B分别为数轴上的两点,A点对应的数为-10,B点对应的数为70.
⑴请写出AB的中点M对应的数
![]()
⑵现在有一只电子蚂蚁P从A点出发,以3个单位/秒的速度向右运动,同时另一只电子蚂蚁Q恰好从B点出发,以2个单位/秒的速度向左运动,设两只电子蚂蚁在数轴上的C点相遇,请你求出C点对应的数 .
⑶若当电子蚂蚁P从A点出发,以3个单位/秒的速度向右运动,同时另一只电子蚂蚁Q恰好从B点出发,以2单位/秒的速度向左运动,经过多长时间两只电子蚂蚁在数轴上相距35个单位长度,并写出此时P点对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )

A. ![]() B.
B. ![]() C. 3 D.
C. 3 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
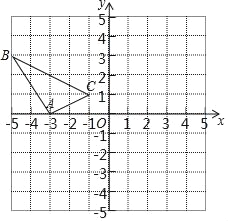
【题目】在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(1)先作△ABC关于原点O成中心对称的△A1B1C1,再把△A1B1C1向上平移4个单位长度得到△A2B2C2;
(2)△A2B2C2与△ABC是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为配合我市创建省级文明城市,某校对八年级各班文明行为劝导志愿者人数进行了统计,各班统计人数有6名、5名、4名、3名、2名、1名共计六种情况,并制作如下两幅不完整的统计图. 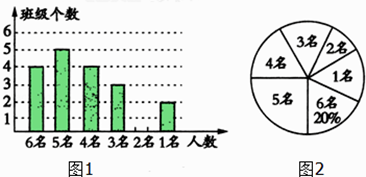
(1)求该年级平均每班有多少文明行为劝导志愿者?并将条形图补充完整;
(2)该校决定本周开展主题实践活动,从八年级只有2名文明行为劝导志愿者的班级中任选两名,请用列表或画树状图的方法,求出所选文明行为劝导志愿者有两名来自同一班级的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com