
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
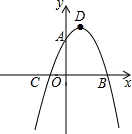 如图,抛物线y=ax2-2ax-3a交y轴于A点,交x轴于B,C两点(B在C右边),顶点为D.
如图,抛物线y=ax2-2ax-3a交y轴于A点,交x轴于B,C两点(B在C右边),顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
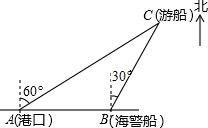 一艘观光游船从港口A以北偏东60°的方向出港观光,航行60海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东30°方向,马上以40海里每小时的速度前往救援,海警船到达事故船C处所需的时间大约为$\frac{\sqrt{3}}{2}$小时(用根号表示).
一艘观光游船从港口A以北偏东60°的方向出港观光,航行60海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东30°方向,马上以40海里每小时的速度前往救援,海警船到达事故船C处所需的时间大约为$\frac{\sqrt{3}}{2}$小时(用根号表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
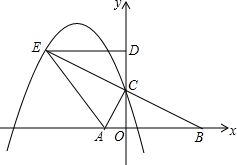 如图,在平面直角坐标系中,已知点A(-1,0)和点B(4,0),点C在y轴正半轴上,且∠ACB=90°,将△COB绕点C旋转180°得到△CDE,连结AE.
如图,在平面直角坐标系中,已知点A(-1,0)和点B(4,0),点C在y轴正半轴上,且∠ACB=90°,将△COB绕点C旋转180°得到△CDE,连结AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com