
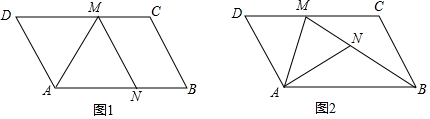
分析 (1)依据翻折的性质和平行线的性质可证明∠DAM=∠DMA,从而可得到DM=AD;
(2)先证明△ANB≌△BCM,依据全等三角形的性质可得到MC=NB,MB=AB=6.5,过点B作BE⊥DC,垂足为E,在Rt△BCE中,利用特殊锐角三角函数值可求得CE=2,BE=2$\sqrt{3}$,在Rt△MBE中,依据勾股定理可求得ME的长,最后依据NB=MC可得到问题的答案.
解答 解:(1)由翻折的性质可知:∠DAM=∠NAM.
∵四边形ABCD为平行四边形,
∴DM∥AN,
∴∠DMA=∠NAM.
∴∠DAM=∠DMA.
∴DM=AD=4.
(2)∵四边形ABCD为平行四边形,∠D=60°,
∴AD=BC,∠DCB=120°.
由翻折的性质可知:AD=AN,∠D=∠MNA=60°.
∴AN=BC,∠ANB=∠MCB=120°.
∵DC∥AB,
∴∠CMB=∠NBA.
在△ANB和△BCM中$\left\{\begin{array}{l}{∠ANB=∠MCB}\\{∠CMB=∠NBA}\\{AN=BC}\end{array}\right.$,
∴△ANB≌△BCM.
∴MC=NB,MB=AB=6.5.
过点B作BE⊥DC,垂足为E.
在Rt△BCE中,∠ECB=60°,BC=4,
∴CE=2,BE=2$\sqrt{3}$.
在Rt△MBE中,ME=$\sqrt{B{M}^{2}-B{E}^{2}}$=$\frac{11}{2}$.
∴NB=MC=$\frac{11}{2}$-2=$\frac{7}{2}$.
点评 本题主要考查的是全等三角形的性质和判定、翻折的性质、特殊锐角三角函数值的应用,勾股定理,掌握本题的辅助线的作法是解题的关键.


科目:初中数学 来源: 题型:选择题
 如图,平面直角坐标系中,直线AD:y=kx+b(k≠0)与x轴交于点B(-2,0),与y轴正半轴交于点C,则关于x的“不等式kx+b≥0的解集”是( )
如图,平面直角坐标系中,直线AD:y=kx+b(k≠0)与x轴交于点B(-2,0),与y轴正半轴交于点C,则关于x的“不等式kx+b≥0的解集”是( )| A. | 射线CD上的点的横坐标的取值范围 | B. | 射线BA上的点的横坐标的取值范围 | ||
| C. | 射线BD上的点的横坐标的取值范围 | D. | 射线CA上的点的横坐标的取值范围 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,动点P从点A出发,以1cm/s的速度向点D运动;动点Q从点C同时出发,以3cm/s的速度向点B运动.规定当其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t,求:
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,动点P从点A出发,以1cm/s的速度向点D运动;动点Q从点C同时出发,以3cm/s的速度向点B运动.规定当其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t,求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com