
【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着-5、-2、1、9,且任意相邻四个台阶上数的和都相等.
(1)求第5个台阶上的数![]() 是多少?
是多少?
(2)求从下到上前31个台阶上数的和;
(3)试用含![]() (
(![]() 为正整数)的式子表示出数“1”所在的台阶数.
为正整数)的式子表示出数“1”所在的台阶数.

【答案】(1)-5;(2)15;(3)4k-1.
【解析】
(1)将前4个数字相加可得;
(2)根据“相邻四个台阶上数的和都相等” 方程求解可得;
(3)根据“台阶上的数是每4个一循环”求解可得;观察发现:由循环规律即可知道“1”所在的台阶数为4k-1.
解:(1)由题意得前4个台阶上的数的和是:-5-2+1+9=3,
∴-2+1+9+x=3,解得:x=-5,则第5个台阶上的数x=-5;
(2)由题意知台阶上的数字是每4个一循环,而31=4×8-1
∴从下到上前31个台阶上的数字和是:8×3-9=15
即从下到上前31个台阶上的数字和是15.
(3)观察发现:数“1”所在的台阶数为3,7,11,15,19…,k为正整数,所以数“1”所在的台阶数为4k-1.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
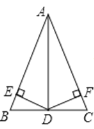
【题目】如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF.
求证:(1)△BDE≌△CDF;
(2)AD是△ABC的角平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
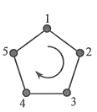
【题目】如图,给正五边形的顶点依次编号 12345,若从某一顶点开始,沿正五边形的边顺时针行走,顶点编号数字是几就走几个边长,则称 这种走法为一次移位,如:小宇在编号为 3 的顶点上时,那么他应该走 3 个边长,即 3-4-5-1 为第一次移位,这时他到达编号为 1 的顶点;然后从 1-2 为第二次移位.若小宇从编号为 2 的顶点开始,第 14 次移位后,则他所处顶点的编号为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
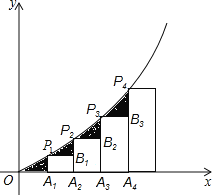
【题目】如图,已知A1,A2,A3,…,An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An-1An=1,分别过点A1,A2,A3,…,An作x轴的垂线交二次函数y=![]() x2(x>0)的图象于点P1,P2,P3,…,Pn.若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3……依次进行下去,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=( )
x2(x>0)的图象于点P1,P2,P3,…,Pn.若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3……依次进行下去,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
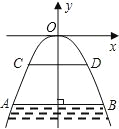
【题目】如图所示,有一座抛物线形拱桥,桥下面在正常水位时,AB宽20 m,水位上升到警戒线CD时,CD到拱桥顶E的距离仅为1 m,这时水面宽度为10 m.
(1)在如图所示的坐标系中求抛物线的解析式;
(2)若洪水到来时,水位以每小时0.3 m的速度上升,从正常水位开始,持续多少小时到达警戒线?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮房间窗户的窗帘如图1所示,它是由两个四分之一圆组成(半径相同)
⑴请用代数式表示装饰物的面积:________,用代数式表示窗户能射进阳光的面积是______(结果保留π)
⑵当a=![]() ,b=1时,求窗户能射进阳光的面积是多少?(取π≈3 )
,b=1时,求窗户能射进阳光的面积是多少?(取π≈3 )
⑶小亮又设计了如图2的窗帘(由一个半圆和两个四分之一圆组成,半径相同),请你帮他算一算此时窗户能射进阳光的面积是否更大?如果更大,那么大多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
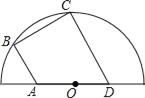
【题目】如图,四边形ABCD内接于半圆O,其中点A,D在直径上,点B,C在半圆弧上,AB∥CD,∠B=90°,若AO=3,∠BAD=120°,则BC=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一辆汽车和一辆摩托车分别从A,B两地去同一城市,l1 ,l2分别表示汽车、摩托车离A地的距离s(km)随时间t(h)变化的图象,则下列结论:①摩托车比汽车晚到1 h;②A,B两地的距离为20 km;③摩托车的速度为45 km/h,汽车的速度为60 km/h;④汽车出发1 h后与摩托车相遇,此时距离B地40 km;⑤相遇前摩托车的速度比汽车的速度快.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,直线l1∥x轴,直线l2为第一、三象限的角平分线,直线l1与l2相交于A(3,3),点B为直越l1上一点,点C为x轴上一点,P(x,y)为一动点.
(1)当点P(x,y)在x轴上时,y= ,当点P(x,y)在直线l1上,y= ,当点P(x,y)在直线l2上时y= .
如图1,当点P在直线l1下方、x轴上方、直线l2左上方区域时,x,y满足如下条件:![]() ,则∠APO,∠PAB,∠POC的数量关系是 .
,则∠APO,∠PAB,∠POC的数量关系是 .
如图2,当点P在直线l1下方、x轴上方、直线l2右下方区域时,x,y满足如下条件:![]() ,则∠APO,∠PAB,∠POC的数量关系是 .
,则∠APO,∠PAB,∠POC的数量关系是 .
(2)当点P在直线l1上方区域,且点P不在直线l2时,x,y满足的条件为:![]() ,请画出图形,猜想∠APO,∠PAB,∠POC的数量关系,并说明理由.
,请画出图形,猜想∠APO,∠PAB,∠POC的数量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com