
【题目】如图,在□ABCD中,AB=26,AD=6,将□ABCD绕点A旋转,当点D的对应点D′落在AB边上时,点C的对应点C′恰好与点B、C在同一直线上,则此时△C′D′B的面积为()

A.120B.240C.260D.480
【答案】B
【解析】
根据平行四边形的性质和旋转的性质可推出∠C′BD′=∠C=∠D′AB′=∠BD′C′,因此可得△C′BD′为等腰三角形,进而可推出△C′BD′的高,即可算出面积.
如图:
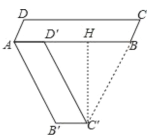
∵□ABCD中绕点A旋转后得到□AB′C′D′,
∴∠DAB=∠D′AB′,AB=AB′=C′D′=26,
∵AB′∥C′D′,
∴∠D′AB′=∠BD′C′,
∵四边形ABCD为平行四边形,
∴∠C=∠DAB,
∴∠C=∠BD′C′,
∵点C′、B、C在一条直线上,而AB//CD,
∴∠C=∠C′BD′,
∴∠C′BD′=∠BD′C′
∴△C′BD′为等腰三角形,
作C′H⊥D′B,则BH=D′H,
∵AB=26,AD=6,
∴BD′=20,
∴D′H=10,
∴C′H=![]() ,
,
∴△C′D′B的面积=![]() ·BD′·C′H=
·BD′·C′H=![]() ×20×24=240,
×20×24=240,
故选:B.


科目:初中数学 来源: 题型:
【题目】在半径为27m的广场中央,点O的上空安装了一个照明光源S,S射向地面的光束呈圆锥形,其轴截面SAB的顶角为120°(如图),求光源离地面的垂直高度SO.(精确到0.1m;![]() =1.44,
=1.44,![]() =1.732,
=1.732,![]() =2.236,以上数据供参考)
=2.236,以上数据供参考)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校6名教师和234名学生外出参加集体活动,学校准备租用45座大车和30座小车若干辆.已知租用1辆大车、2辆小车的租车费用是1000元,租用2辆大车、1辆小车的租车费用是100元.
(1)每辆大车、小车的租车费用各是多少元?
(2)学校要求每辆车上至少要有一名教师,且租车总费用不超过2300元,请问有几种符合条件的租车方案?哪种租车方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求△MCB的面积S△MCB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为一台灯示意图,其中灯头连接杆DE始终和桌面FG平行,灯脚AB始终和桌面FG垂直,

(1)当∠EDC=∠DCB=120°时,求∠CBA;
(2)连杆BC、CD可以绕着B、C和D进行旋转,灯头E始终在D左侧,设∠EDC,∠DCB,∠CBA的度数分别为α,β,γ,请画出示意图,并直接写出示意图中α,β,γ之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBEF是菱形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=ax+b的图象上有两点A、B,它们的横坐标分别是3,-1,若二次函数y=![]() x2的图象经过A、B两点.
x2的图象经过A、B两点.
(1)请求出一次函数的表达式;
(2)设二次函数的顶点为C,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com