
七年级我们曾学过“两点之间线段最短”的知识,常可利用它来解决两条线段和最小的相关问题,下面是大家非常熟悉的一道习题:
如图1,已知,A,B在直线l的同一侧,在l上求作一点,使得PA+PB最小.
|
|


我们只要作点B关于l的对称点B′,(如图2所示)根据对称性可知,PB=PB'.因此,求AP+BP最小就相当于求AP+PB′最小,显然当A、P、B′在一条直线上时AP+PB′最小,因此连接AB',与直线l的交点,就是要求的点P.
有很多问题都可用类似的方法去思考解决.
探究:
1.如图3,正方形ABCD的边长为2,E为BC的中点, P是BD上一动点.连结EP,CP,则EP+CP的最小值是________;

运用:
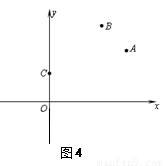
2.如图4,平面直角坐标系中有三点A(6,4)、B(4,6)、C(0,2),在x轴上找一点D,使得四边形ABCD的周长最小,则点D的坐标应该是 ;
操作:
3.如图5,A是锐角MON内部任意一点,在∠MON的两边OM,ON上各求作一点B,C,组成△ABC,使△ABC周长最小.(不写作法,保留作图痕迹)

科目:初中数学 来源: 题型:
| 5 |
| 5 |

查看答案和解析>>
科目:初中数学 来源: 题型:
|
|

 我们只要作点B关于l的对称点B′,(如图2所示)根据对称性可知,PB=PB'.因此,求AP+BP最小就相当于求AP+PB′最小,显然当A、P、B′在一条直线上时AP+PB′最小,因此连接AB',与直线l的交点,就是要求的点P.
我们只要作点B关于l的对称点B′,(如图2所示)根据对称性可知,PB=PB'.因此,求AP+BP最小就相当于求AP+PB′最小,显然当A、P、B′在一条直线上时AP+PB′最小,因此连接AB',与直线l的交点,就是要求的点P.


查看答案和解析>>
科目:初中数学 来源:2012届江苏省南京市溧水县中考一模数学试卷(带解析) 题型:解答题
七年级我们曾学过“两点之间线段最短”的知识,常可利用它来解决两条线段和最小的相关问题,下面是大家非常熟悉的一道习题:
如图1,已知,A,B在直线l的同一侧,在l上求作一点,使得PA+PB最小.
|
|

 我们只要作点B关于l的对称点B′,(如图2所示)根据对称性可知,PB=PB'.因此,求AP+BP最小就相当于求AP+PB′最小,显然当A、P、B′在一条直线上时AP+PB′最小,因此连接AB',与直线l的交点,就是要求的点P.
我们只要作点B关于l的对称点B′,(如图2所示)根据对称性可知,PB=PB'.因此,求AP+BP最小就相当于求AP+PB′最小,显然当A、P、B′在一条直线上时AP+PB′最小,因此连接AB',与直线l的交点,就是要求的点P.


查看答案和解析>>
科目:初中数学 来源:2012年江苏省南京市溧水县中考数学一模试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2012年江苏省常州市外国语学校中考数学三模试卷(5月份)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com