
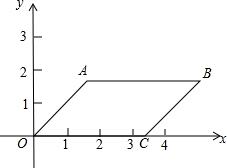
 如图,在平行四边形OABC中,已知AB=OC,AB∥OC.A、C两点的坐标分别为$A(\sqrt{3},\sqrt{3}),C(2\sqrt{3},0)$.
如图,在平行四边形OABC中,已知AB=OC,AB∥OC.A、C两点的坐标分别为$A(\sqrt{3},\sqrt{3}),C(2\sqrt{3},0)$.分析 (1)根据平行四边形的性质AB=OC=2$\sqrt{3}$,由此即可解决问题.
(2)根据向左平移纵坐标不变,横坐标减去$\sqrt{3}$即可.
(3)根据平行四边形的面积公式计算即可.
解答 解:(1)在平行四边形OABC中,已知A、C两点的坐标分别为$A(\sqrt{3},\sqrt{3}),C(2\sqrt{3},0)$. ∵AB=OC=2$\sqrt{3}$,$\sqrt{3}$+2$\sqrt{3}$=3$\sqrt{3}$,
∵AB=OC=2$\sqrt{3}$,$\sqrt{3}$+2$\sqrt{3}$=3$\sqrt{3}$,
∴B点的坐标是(3$\sqrt{3}$,$\sqrt{3}$).
(2)将平行四边形OABC向左平移$\sqrt{3}$个单位长度,所得四边形的四个顶点的
坐标分别是:(0,$\sqrt{3}$),(2$\sqrt{3}$,$\sqrt{3}$),($\sqrt{3}$,0),(-$\sqrt{3}$,0).
(3)平行四边形OABC的面积=2$\sqrt{3}$×$\sqrt{3}$=6.
点评 本题考查四边形综合题、坐标与点的位置关系、平行四边形的性质等知识,解题的关键是熟练掌握平行四边形的性质,记住平行四边形的面积等于底乘高,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
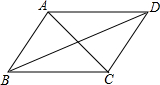 如图,下列条件不能够判定AB∥DC的是( )
如图,下列条件不能够判定AB∥DC的是( )| A. | ∠BAC=∠ACD | B. | ∠DCB+∠ABC=180° | C. | ∠ABD=∠BDC | D. | ∠DAC=∠BCA |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
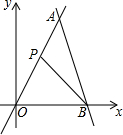 如图,在平面直角坐标系中,直线OA的函数表达式为y=2x,直线AB的函数表达式为y=-3x+b,点B的坐标为$(\frac{10}{3},0)$.点P沿折线OA-AB运动,且不与点O和点B重合.设点P的横坐标为m,△OPB的面积为S.
如图,在平面直角坐标系中,直线OA的函数表达式为y=2x,直线AB的函数表达式为y=-3x+b,点B的坐标为$(\frac{10}{3},0)$.点P沿折线OA-AB运动,且不与点O和点B重合.设点P的横坐标为m,△OPB的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12×0.8-x=2 | B. | 12-x×0.8=2 | C. | (12-x)×0.8=2 | D. | 12-x=2×0.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com