
【题目】某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(单位:千帕)随气体体积V(单位:立方米)的变化而变化,P随V的变化情况如下表所示.
P | 1.5 | 2 | 2.5 | 3 | 4 | … |
V | 64 | 48 | 38.4 | 32 | 24 | … |
(1)写出符合表格数据的P关于V的函数表达式 ;
(2)当气球的体积为20立方米时,气球内气体的气压P为多少千帕?
(3)当气球内的气压大于144千帕时,气球将爆炸,依照(1)中的函数表达式,基于安全考虑,气球的体积至少为多少立方米?
【答案】(1)p=![]() ;(2)4.8千帕;(3)气球的体积应不小于
;(2)4.8千帕;(3)气球的体积应不小于![]() 立方米.
立方米.
【解析】
(1)设p与V的函数的解析式为p=![]() ,利用待定系数法即可求函数解析式;
,利用待定系数法即可求函数解析式;
(2)把v=20代入p=![]() 可得p=4.8;
可得p=4.8;
(3)把p=144代入p=![]() 得,V=
得,V=![]() .可知当气球内的气压>144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于
.可知当气球内的气压>144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于![]() 立方米.
立方米.
解:(1)设p与V的函数的解析式为p=![]() ,
,
把点A(1.5,64)代入,
解得k=96.
∴这个函数的解析式为p=![]() ;
;
故答案为:p=![]() ;
;
(2)把v=20代入p=![]() 得:p=4.8,
得:p=4.8,
当气球的体积为20立方米时,气球内的气压是4.8千帕;
(3)把p=144代入p=![]() 得,V=
得,V=![]() ,
,
故p≤144时,v≥![]() ,
,
答:气球的体积应不小于![]() 立方米.
立方米.
故答案为:(1)p=![]() ;(2)4.8千帕;(3)气球的体积应不小于
;(2)4.8千帕;(3)气球的体积应不小于![]() 立方米.
立方米.


科目:初中数学 来源: 题型:
【题目】甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为![]() (元),在乙采摘园所需总费用为
(元),在乙采摘园所需总费用为![]() (元),图中折线OAB表示
(元),图中折线OAB表示![]() 与x之间的函数关系.
与x之间的函数关系.

(1)甲、乙两采摘园优惠前的草莓销售价格是每千克 元;
(2)求![]() 、
、![]() 与x的函数表达式;
与x的函数表达式;
(3)在图中画出![]() 与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围.
与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2,两块绿地之间及周边有宽度相等的人行通道,设人行通道的宽度为xm,则可列方程为_____.
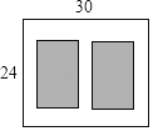
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,E是边BC上的点,将线段DE绕点E逆时针旋转90°得到EF,过点C作CG∥EF交BA(或其延长线)于点G,连接DF,FG.
(1)FG与CE的数量关系是 ,位置关系是 .
(2)如图2,若点E是CB延长线上的点,其它条件不变.
①(1)中的结论是否仍然成立?请作出判断,并给予证明;
②DE,DF分别交BG于点M,N,若BC=2BE,求![]() .
.
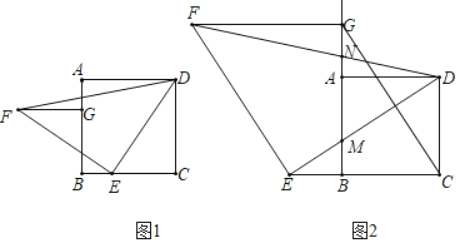
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O内切于Rt△ABC,点P、点Q分别在直角边BC、斜边AB上,PQ⊥AB,且PQ与⊙O相切,若AC=2PQ,则tan∠B的值为( )
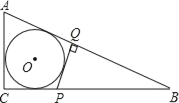
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(![]() ,﹣2);⑤当x<
,﹣2);⑤当x<![]() 时,y随x的增大而减小;⑥a+b+c>0;⑦方程ax2+bx+c=﹣4有实数解,正确的有( )
时,y随x的增大而减小;⑥a+b+c>0;⑦方程ax2+bx+c=﹣4有实数解,正确的有( )
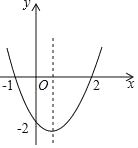
A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
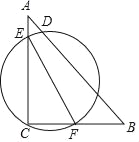
【题目】如图,△ABC中,∠C=90°,AC=8,BC=6,E,F分别在边AC,BC,若以EF为直径作圆经过AB上某点D,则EF长的取值范围为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com