
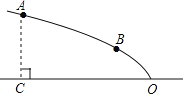
����Ŀ����ͼ��ij�㳡��Ƶ�һ���������͵��ݽ����������ߵ�һ���֣������ߵĶ���O����ˮƽ���ϣ��Գ�����ˮƽ��OC����A��B�������������ϣ��ҵ�A��ˮƽ��ľ���AC=4�ף���B��ˮƽ�����Ϊ2�ף�OC=8�ף�
��1���뽨���ʵ���ֱ������ϵ���������ߵĺ�������ʽ��
��2��Ϊ�˰�ȫ���ۣ�������ˮƽ��OC����һ��P�����ʵء������ȷ����Բ�θֹ���������֧��PA��PB�����������ͽ���֧�żӹ̣���ô���������ҵ�����֧��������ʡ��֧������桢���ͶԽӷ�ʽ�����϶��������ݲ����ǣ�ʱ�ĵ�P��������֤����
��3��Ϊ��ʩ�����㣬����������O��P֮��ľ��룬��ô����֧��������ʡʱ��O��P֮��ľ����Ƕ��٣�����д�����̣�
���𰸡���1�������ߵĽ���ʽΪ��x=��![]() y2+8��
y2+8��
��2������A���ڵ�C�ĶԳƵ��D������DB��x�ύ�ڵ�P�����P��Ϊ����
��3������֧��������ʡʱ��O��P֮��ľ�����4�ף�
��������
�����������1������������Խ������ʵ�ƽ��ֱ������ϵ���Ӷ�������������ߵĽ���ʽ��
��2����������֮���߶���࣬������Ӧ��ͼ�Σ�д���������ɣ�
��3������ǰ�������ϵ�������߽���ʽ������õ�B�����꣬�ٸ������������ƿ����������֧��������ʡʱ��O��P֮��ľ��룬ע��˴�ֻд���𰸼��ɣ�
�⣺��1������ͼ��ʾ��
������ɵã���C������Ϊ��0��0������A������Ϊ��0��4������O������Ϊ��8��0����
��������ߵĽ���ʽΪ��x=ay2+8��
��0=a��42+8��
��ã�a=��![]() ��
��
�������ߵĽ���ʽΪ��x=��![]() y2+8��
y2+8��
��2������A���ڵ�C�ĶԳƵ��D������DB��x�ύ�ڵ�P�����P��Ϊ����
��3������֧��������ʡʱ��O��P֮��ľ�����4�ף�



 �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д� ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д� һ���㶨ϵ�д�
һ���㶨ϵ�д� ��У��ҵ��ϵ�д�
��У��ҵ��ϵ�д� ���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һԪ���η���x2+x��2=0�ĸ�������ǣ� ��
A.����������ȵ�ʵ����
B.��������ȵ�ʵ����
C.ֻ��һ��ʵ����
D.û��ʵ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�У���BAD=130�㣬��B=��D=90�㣬��BC��CD�Ϸֱ���һ��M��N��ʹ������AMN�ܳ���Сʱ�����AMN+��ANM�Ķ���Ϊ��������

A. 80�� B. 90�� C. 100�� D. 130��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һֻ���ϴ�������A���������3����λ���ȵ���-1�㣬���A����ʾ�������� ��
A. 2 B. -4 C. 2��-4 D. ��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y����5x��3��ͼ������������( )
A. ��һ���� B. �ڶ����� C. �������� D. ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
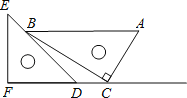
����Ŀ��һ��ֱ�����ǰ���ͼ���ã���C��FD���ӳ����ϣ�AB��CF����F=��ACB=90�㣬��E=45�㣬��A=60�㣬AC=10������CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У��㣨��1����2���ڣ�������
A. ��һ���� B. �ڶ����� C. �������� D. ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�κ���y=kx+b��ͼ����P����2��3������2k��b��ֵΪ�� ��
A.2
B.��2
C.3
D.��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ����֪������������y1=kx��k��0���뷴��������y2=![]() ��m��0��ͼ���ཻ��A��B���㣬�������ֱ���1�ͩ�1����ʽkx��
��m��0��ͼ���ཻ��A��B���㣬�������ֱ���1�ͩ�1����ʽkx��![]() �Ľ⼯������������⣬ijͬѧ���������ģ�����ͼ���֪����x��1��1��x��0ʱ��y1��y2�����Բ���ʽkx��
�Ľ⼯������������⣬ijͬѧ���������ģ�����ͼ���֪����x��1��1��x��0ʱ��y1��y2�����Բ���ʽkx��![]() �Ľ⼯��x��1��1��x��0���������ֽ�������˼·���ֵ���ѧ˼�뷽���ǣ� ��
�Ľ⼯��x��1��1��x��0���������ֽ�������˼·���ֵ���ѧ˼�뷽���ǣ� ��
A�����ν�� B��ת�� C����� D����������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com