
【题目】莫小贝在襄阳北街租了一家商铺专门销售各种旅游纪念品.本月初他在进货时发现:若购进甲种纪念品 3
件,乙种纪念品 2 件,需要 400 元,若购进甲种纪念品 4 件,乙种纪念品 5 件,需要 650 元. (1)求购进甲乙两种纪念品每件各需要多少元?
(2)若莫小贝决定购进这两种纪念品共 100 件,其中甲种纪念品的数量不少于 65 件.考虑到资金周转,用于购 买这些纪念品的资金不超过 9000 元,那么莫小贝共有几种进货方案?
(3)若每卖出一件甲种纪念品可获利润 20 元,一件乙种纪念品可获利润 35 元.在(2)的条件下,所购的 100 件 纪念品可以全部销售完,怎样进货才能使得获得的利润最大?最大利润是多少元?
【答案】(1)甲种纪念品每件需要 100 元,乙种纪念品每件需要 50 元;(2)莫小贝共有 16 种进货方案;(3)购进甲种 65 件、乙种 35 件时获得最大利润 2525 元.
【解析】(1)设甲种纪念品每件需要 x 元,乙种纪念品每件需要 y 元,根据购进甲种纪念品 3件,乙种纪念品 2 件,需要 400 元,若购进甲种纪念品 4 件,乙种纪念品 5 件,需要 650 元列出方程组,求出x,y的值即可;
(2)设购进甲种纪念品 m 件,则购进乙种纪念品(100-m)件,根据购进甲种纪念品的数量不少于 65 件和购 买这些纪念品的资金不超过 9000 元,列出不等式组,求出m的取值范围,再根据m只能取整数,得出进货方案;
(3)设 100 件纪念品全部销售后的利润为 w 元,列出函数关系式求解即可.
(1)设甲种纪念品每件需要 x 元,乙种纪念品每件需要 y 元, 根据题意可得![]() ,
,
解得![]() ,
,
答:甲种纪念品每件需要 100 元,乙种纪念品每件需要 50 元;
(2)设购进甲种纪念品 m 件,则购进乙种纪念品(100-m)件,
根据题意可得 ![]() , 解得 65≤m≤80,
, 解得 65≤m≤80,
∵m 取整数
∴m=65,66,67……78;79;80 共 16 种, 答:莫小贝共有 16 种进货方案;
(3)设 100 件纪念品全部销售后的利润为 w 元,
w=20m+35(100-m)
=-15m+3500
∵k=-15<0,
∴w 随着 m 的增大而减小,
∴当 m=65 时,w 有最大值, 此时 w=-15×65+3500
答:购进甲种 65 件、乙种 35 件时获得最大利润 2525 元.


科目:初中数学 来源: 题型:
【题目】铁路货运调度站有A、B两个信号灯,在灯这旁停靠着甲、乙、丙三列火车.它们中最长的车长与居中车长之差等于居中车长与最短车长之差,其中乙车的车长居中,最开始的时候,甲、丙两车车尾对齐,且车尾正好位于A信号灯处,而车头则冲着B信号灯的方向,乙车的车尾则位于B信号灯处,车头则冲着A的方向,现在,三列火车同时出发向前行驶,3秒之后三列火车的车头恰好相遇,再过9秒,甲车恰好超过丙车,而丙车也正好完全和乙车错开,请问:甲乙两车从车头相遇直到完全错开一共用了_____秒钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC的中点.
(1)求证:四边形AEDF是菱形;
(2)如果四边形AEDF的周长为12,两条对角线的和等于7,求四边形AEDF的面积S.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了从甲乙两人中选拔一人参加初中数学竞赛,每个月对他们进行一次测试,如图绘出了两个人赛前 5 次测验成绩(每次测验成绩都是 5 的倍数).
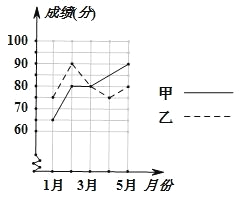
(1)分别求出甲乙两人 5 次测验成绩的平均数与方差;
(2)如果你是他们的辅导老师,应该选拔哪位学生参加这次竞赛,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
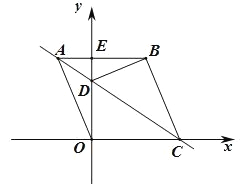
【题目】如图,四边形 ABCO 是菱形,以点 O 为坐标原点,OC 所在直线为![]() 轴建立平面直角坐标系.若点 A 的坐 标为(-5,12),直线 AC、边 AB 与
轴建立平面直角坐标系.若点 A 的坐 标为(-5,12),直线 AC、边 AB 与![]() 轴的交点分别是点 D 与点 E,连接 BD.
轴的交点分别是点 D 与点 E,连接 BD.
(1)求菱形 ABCO 的边长;
(2)求 BD 所在直线的解析式;
(3)直线 AC 上是否存在一点 P 使得![]() 与
与![]() 的面积相等?若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
的面积相等?若存在,请直接写出点 P 的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A,B两点,分别代表﹣40,20,两只电子蚂蚁甲,乙分别从AB两点同时出发,甲沿线段AB以3个单位长度/秒的速度向右运动,甲到达点B处时运动停止,乙沿BA方向以5个单位长度/秒的速度向左运动.
![]()
(1)A,B两点间的距离为 个单位长度;甲到达B点时共运动了 秒.
(2)甲,乙在数轴上的哪个点相遇?
(3)多少秒时,甲、乙相距28个单位长度?
(4)若乙到达A点后立刻掉头并保持速度不变,则甲到达B点前,甲,乙还能在数轴上相遇吗?若能,求出相遇点所对应的数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A,B在数轴上表示的数分别为a,b,且|a+6|+(b-18)2=0(规定:数轴上A,B两点之间的距离记为AB).
(1)求b-a的值.
(2)数轴上是否存在点C,使得CA=3CB?若存在,请求出点C所表示的数;若不存在,请说明理由.
(3)动点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,动点Q从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,且P比Q先运动2秒.问点Q运动多少秒时,P,Q相距4个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图象中所反应的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法错误的是( )
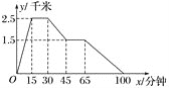
A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是![]() 千米/小时
千米/小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com