
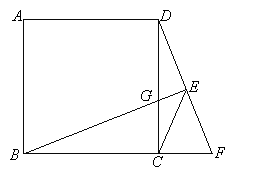
【题目】在正方形ABCD 中,点F是BC延长线上一点,过点B作BE⊥DF于点E,交CD于点G,连接CE.
(1)若正方形ABCD边长为3,DF=4,求CG的长;
(2)求证:EF+EG=![]() CE.
CE.
【答案】(1) ![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题(1)根据正方形的性质可得∠BCG=∠DCB=∠DCF=90°,BC=DC,再根据同角的余角相等求出∠CBG=∠CDF,然后利用“角边角”证明△CBG和△CDF全等,根据全等三角形对应边相等可得BG=DF,再利用勾股定理列式计算即可得解;
(2)过点过点C作CM⊥CE交BE于点M,根据全等三角形对应边相等可得CG=CF,全等三角形对应角相等可得∠F=∠CGB,再利用同角的余角相等求出∠MCG=∠ECF,然后利用“角边角”证明△MCG和△ECF全等,根据全等三角形对应边相等可得MG=EF,CM=CE,从而判断出△CME是等腰直角三角形,再根据等腰直角三角形的性质证明即可.
试题解析:(1)解:∵四边形ABCD是正方形,
∴∠BCG=∠DCB=∠DCF=90°,BC=DC,
∵BE⊥DF,
∴∠CBG+∠F=∠CDF+∠F,
∴∠CBG=∠CDF,
在△CBG和△CDF中,
 ,
,
∴△CBG≌△CDF(ASA),
∴BG=DF=4,
∴在Rt△BCG中,CG2+BC2=BG2,
∴CG=![]() ;
;
(2)证明:如图,过点C作CM⊥CE交BE于点M,

∵△CBG≌△CDF,
∴CG=CF,∠F=∠CGB,
∵∠MCG+∠DCE=∠ECF+∠DCE=90°,
∴∠MCG=∠ECF,
在△MCG和△ECF中,
 ,
,
∴△MCG≌△ECF(SAS),
∴MG=EF,CM=CE,
∴△CME是等腰直角三角形,
∴ME=![]() CE,
CE,
又∵ME=MG+EG=EF+EG,
∴EF+EG=![]() CE.
CE.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
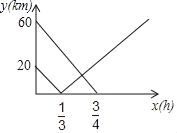
【题目】在连接A、B两市的公路之间有一个机场C,机场大巴由A市驶向机场C,货车由B市驶向A市,两车同时出发匀速行驶,图中线段、折线分别表示机场大巴、货车到机场C的路程y(km)与出发时间x(h)之间的函数关系图象.
(1)直接写出连接A、B两市公路的路程以及货车由B市到达A市所需时间.
(2)求机场大巴到机场C的路程y(km)与出发时间x(h)之间的函数关系式.
(3)求机场大巴与货车相遇地到机场C的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
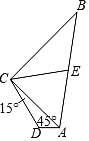
【题目】已知四边形ABCD中,AB=10,BC=8,CD=![]() ∠DAC=45°,∠DCA=15°.
∠DAC=45°,∠DCA=15°.
(1)求△ADC的面积;
(2)若E为AB的中点,求线段CE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个多边形沿着几条直线剪开,分割成若干个多边形.分割后的多边形的边数总和比原多边形的边数多13条,内角和是原多边形内角和的1.3倍.求:(多边形的内角和公式:(n-2)·180)
(1)原来的多边形是几边形?
(2)把原来的多边形分割成了多少个多边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用三个正方形①、2个正方形②、1个正方形③和缺了一个角的长方形④,恰好拼成一个大长方形.根据图示数据,解答下列问题:
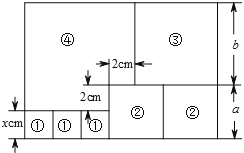
(1)用含x的代数式表示:a=__________cm,b=__________cm;
(2)用含x的代数式表示大长方形的周长,并求x=5时大长方形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“抢红包”是2015年春节十分火爆的一项网络活动,某企业有4000名职工,从中随机抽取350人,按年龄分布和“抢红包”所持态度情况进行调查,并将调查结果绘成了条形统计图和扇形统计图.
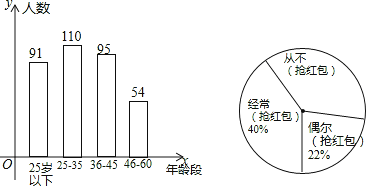
(1)这次调查中,如果职工年龄的中位数是整数,那么这个中位数所在的年龄段是哪一段?
(2)如果把对“抢红包”所持态度中的“经常(抢红包)”和“偶尔(抢红包)”统称为“参与抢红包”,那么这次接受调查的职工中“参与抢红包”的人数是多少?并估计该企业“从不(抢红包)”的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点C.抛物线
与x轴交于点A,与y轴交于点C.抛物线![]() 经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
经过A,C两点,且与x轴交于另一点B(点B在点A右侧).

(1)求抛物线的解析式及点B坐标;
(2)若点M是线段BC上的一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;
(3)试探究当ME取最大值时,在抛物线上、x轴下方是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).

(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是最小的正整数,且
是最小的正整数,且![]() 满足
满足![]() ,请回答:
,请回答:
(1)请直接写出![]() 的值:
的值:![]() =______,
=______,![]() =______,
=______,![]() =______;
=______;
(2)在(1)的条件下,若点P为一动点,其对应的数为![]() ,点P在0到2之间运动,即
,点P在0到2之间运动,即![]() 时,化简:
时,化简:![]() ;
;
(3)在(1)(2)的条件下,![]() ,b,c分别对应的点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,假设
,b,c分别对应的点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,假设![]() 秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间
秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com