
分析 设AD=x,再根据折叠的性质得∠PDE=∠ADE=90°,∠1=∠A,PD=AD=x,于是可判断点P在边AC上,所以PC=20-2x,然后利用等角的余角相等得到∠1=∠3,则∠A=∠3,则可判断Rt△BCP∽Rt△ABC,利用相似比可计算出x.
解答 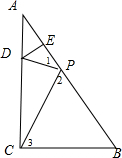 解:如图,设AD=x,
解:如图,设AD=x,
在△ABC中,∠ACB=90°,BC=15,AC=20,
∴AB=25,
∵DE⊥AB,
∴∠AED=∠ACB=90°,
∵△ADE沿DE翻折得到△PDE
∴∠PED=∠AED=90°,∠1=∠A,PD=AD=x,
∴CD=20-x,
∵∠CPD=90°,
∴∠1+∠2=90°,∠A+∠B=90°,
∴∠2=∠B,
∴PC=BC=15,
∵CD2=CP2+PD2,
即(20-x)2=152+x2,
∴x=$\frac{35}{8}$,
∴AD=$\frac{35}{8}$.
故答案为:$\frac{35}{8}$.
点评 此题主要考查了图形的翻折变换,以及勾股定理的应用,关键是掌握翻折后哪些线段是对应相等的.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:解答题
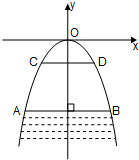 有一座抛物线形拱桥,以坐标原点O为抛物线的顶点,以y轴为抛物线的对称轴建立如图所示的坐标系,桥下面在正常水位AB时,宽20米,水位上升3米就达到警戒线CD,这时水面宽为10米.求抛物线的解析式及警戒线CD到拱桥顶O的距离.
有一座抛物线形拱桥,以坐标原点O为抛物线的顶点,以y轴为抛物线的对称轴建立如图所示的坐标系,桥下面在正常水位AB时,宽20米,水位上升3米就达到警戒线CD,这时水面宽为10米.求抛物线的解析式及警戒线CD到拱桥顶O的距离.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | $-\frac{2}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
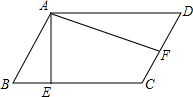 如图,已知?ABCD中,AE⊥BC,AF⊥DC,BC:CD=3:2,AB=EC,则∠EAF=( )
如图,已知?ABCD中,AE⊥BC,AF⊥DC,BC:CD=3:2,AB=EC,则∠EAF=( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com