Question

3．问题情境：已知矩形ABCD中，AD=8，AB=6，点E是线段BC上的一个动点，连接AE，并延长交射线DC于点F，将△ABE沿直线AE翻折，点B落在点B′处，延长AB′，交直线CD于点M．
自主探究：
（1）当$\frac{BE}{CE}$=1时，得到图1，求CF的长并求证：AM=FM．
（2）当点B′恰好落在对角线AC上时，得到图2，此时CF的长为10，$\frac{BE}{CE}$=$\frac{3}{5}$．当$\frac{BE}{CE}$=2时，借助备用图直接写出MF的长为$\frac{145}{18}$．
拓展运用：
（3）设变量BE为x，△ABE沿直线AE翻折后与矩形ABCD重合部分的面积为y，求y与x之间的关系式并直接写出x的取值范围．

Answer 1

分析 （1）①利用相似三角形的判定与性质得出FC=AB即可得出答案；
②利用翻折变换的性质得出∠BAF=∠MAF，进而得出AM=FM；
（2）根据翻折变换的性质得出∠BAE=∠MAF，进而根据AM=MF，利用△ABE∽FCE得出答案即可；
（3）分两种情况：①当0＜x≤6时；②当6＜x≤8时；利用三角形的面积和勾股定理探讨得出答案即可．

解答 （1）解：∵四边形ABCD是矩形，
∴AB∥DC．
∴∠B=∠BCF．
∵∠AEB=∠FEC，
∴△ABE∽△FCE．…（1分）
∴$\frac{AB}{FC}$=$\frac{BE}{CE}$，
∵$\frac{BE}{CE}$=1，
∴$\frac{AB}{FC}$=$\frac{BE}{CE}$=1，AB=CF．
∵AB=6，
∴CF=6．
证明：∵AB∥DC，
∴∠BAF=∠AFC．
∵△ABE沿直线AE翻折得到△AB’E，
∴∠BAF=∠MAF，
∴∠MAF=∠AFC．
∴AM=FM．

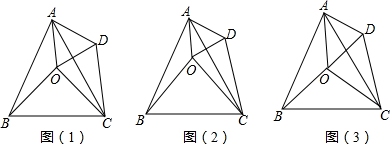
（2）解：如图2，

∵当点B′恰好落在对角线AC上时，
∴∠1=∠2，
∵AB∥FC，
∴∠1=∠F，
∴∠2=∠F，
∴AC=FC=10，
∵AB=6，BC=，8，
∴AC=FC=10，
∵AB∥FC，
∴△ABE∽FCE，
∴$\frac{BE}{EC}$=$\frac{AB}{FC}$=$\frac{6}{10}$=$\frac{3}{5}$；
如图，

∵AB∥CF，
∴△ABE∽△FCE，
∴$\frac{BE}{CE}$=$\frac{AB}{CF}$=2，
∵AB=6，
∴CF=3，
∴DF=CD+CF=9，
由（1）知：AM=FM，
∴AM=FM=9-DM，
在Rt△ADM中，由勾股定理得：DM²=（9-DM）²-8²，
解得：DM=$\frac{17}{18}$，则MA=$\frac{145}{18}$．
（3）解：分类讨论如下：
①当0＜x≤6时，如图：

∵BE=x，
∴y=S_△AB’E=S_△ABE=$\frac{1}{2}$BE•AB=$\frac{1}{2}$•x•6=3x．
②当6＜x≤8时，如图：

∵△ABE沿直线AE翻折得到△AB′E
∴∠AEB=∠AEB′，BE=B′E，AB=AB′=6．
∵四边形ABCD是矩形，
∴AD∥BC．
∴∠AEB=∠EAD．
∴∠AEB′=∠EAD．
∴AH=EH．
∴AH+B′H=B′E=BE=x．
在Rt△AB′H中，由勾股定理得6²+（x-EH）²=EH²．
解得EH=$\frac{x}{2}$+$\frac{18}{x}$．
∴y=S_△AEH=$\frac{1}{2}$EH•AB=$\frac{1}{2}$×6×（$\frac{x}{2}$+$\frac{18}{x}$）=$\frac{3x}{2}$+$\frac{54}{x}$．
综上所述，y与x的函数关系为y=$\left\{\begin{array}{l}{3x（0＜x≤6）}\\{\frac{3}{2}x+\frac{54}{x}（6＜x≤8）}\end{array}\right.$．

点评 此题主要考查了几何变换综合题，翻折变换的性质以及相似三角形的判定与性质和勾股定理等知识，熟练利用相关性质和进行分类讨论得出是解题关键．