
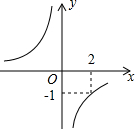
 已知函数y与自变量x之间的关系如图所示,那么y与x之间的函数关系式为y=-$\frac{2}{x}$,如果P(-4,c)在这个函数的图象上,那么c值为$\frac{1}{2}$.
已知函数y与自变量x之间的关系如图所示,那么y与x之间的函数关系式为y=-$\frac{2}{x}$,如果P(-4,c)在这个函数的图象上,那么c值为$\frac{1}{2}$. 科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
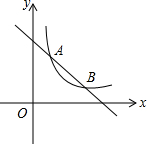 如图,在平面直角坐标系中,一次函数y=-x+m与反比例函数$y=\frac{k}{x}$的图象交于点A(1,3a),B(3,a).
如图,在平面直角坐标系中,一次函数y=-x+m与反比例函数$y=\frac{k}{x}$的图象交于点A(1,3a),B(3,a).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省盐城市盐都区西片七年级下学期第一次月考数学试卷(解析版) 题型:解答题
【问题背景】
(1)如图1的图形我们把它称为“8字形”,请说明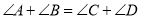 ;
;
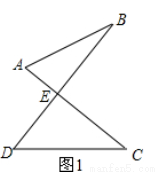
【简单应用】
(2)阅读下面的内容,并解决后面的问题:如图2, AP、CP分别平分∠BAD. ∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数;

【解析】
∵AP、CP分别平分∠BAD. ∠BCD
∴∠1=∠2,∠3=∠4
由(1)的结论得: 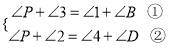
①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D
∴∠P =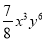 (∠B+∠D)=26°.
(∠B+∠D)=26°.
【问题探究】如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想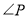 的度数,并说明理由.
的度数,并说明理由.

【拓展延伸】
① 在图4中,若设∠C=α,∠B=β,∠CAP=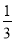 ∠CAB,∠CDP=
∠CAB,∠CDP=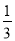 ∠CDB,试问∠P与∠C、∠B之间的数量关系为:________________(用α、β表示∠P),
∠CDB,试问∠P与∠C、∠B之间的数量关系为:________________(用α、β表示∠P),
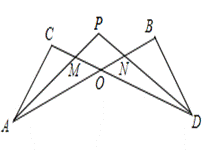
②在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论______________________

查看答案和解析>>
科目:初中数学 来源:2016-2017学年湖北省武汉市侏儒山街四校七年级3月月考数学试卷(解析版) 题型:单选题
下列说法正确的个数是( )
①同一平面内,过一点有且只有一条直线与已知直线垂直;
②同一平面内,过一点有且只有一条直线与已知直线平行;
③若三条直线a⊥c,b⊥c,则a∥b;
④9的平方根是3;
⑤﹣2是4的平方根;
⑥平方根等于本身的数是0和1.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com