
【题目】已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.
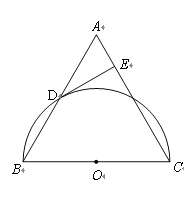
求证:(1)△ABC是等边三角形;
(2)![]() .
.
科目:初中数学 来源: 题型:
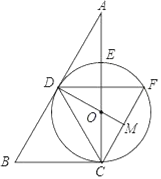
【题目】如图,在△ABC中,点O在边AC上,⊙O与△ABC的边AC,AB分别切于C、D两点,与边AC交于点E,弦![]() 与AB平行,与DO的延长线交于M点.
与AB平行,与DO的延长线交于M点.
(1)求证:点M是CF的中点;
(2)若E是![]() 的中点,连结DF,DC,试判断△DCF的形状;
的中点,连结DF,DC,试判断△DCF的形状;
(3)在(2)的条件下,若BC=a,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种电热淋浴器的水箱盛满水时有200升,加热到一定温度即可供淋浴用,在放水的同时自动注水,设t分钟内注水2t2升,放水34t升,当水箱内的水量达到最小值时,必须停止放水并将水箱注满,加热升温,过一定时间后,才能继续放水使用,现规定每人洗浴用水量不得超过60升,请回答下列问题:
(1)求水箱内水量的最小值;
(2)说明该淋浴器一次可连续供几人洗浴.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列要求,解答相关问题:
(1)请补全以下求不等式﹣2x2﹣4x≥0的解集的过程
①构造函数,画出图象:
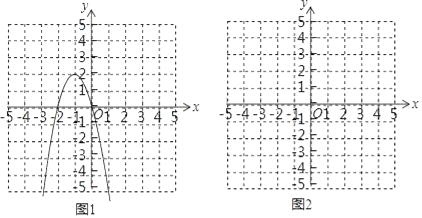
根据不等式特征构造二次函数y=﹣2x2﹣4x;抛物线的对称轴x=﹣1,开口向下,顶点(﹣1,2)与x轴的交点是(0,0),(﹣2,0),用三点法画出二次函数y=﹣2x2﹣4x的图象如图1所示;
②数形结合,求得界点:
当y=0时,求得方程﹣2x2﹣4x=0的解为 ;
③借助图象,写出解集:
由图象可得不等式﹣2x2﹣4x≥0的解集为 .
(2)利用(1)中求不等式解集的方法步骤,求不等式x2﹣2x+1<4的解集.
①构造函数,画出图象;
②数形结合,求得界点;
③借助图象,写出解集.
(3)参照以上两个求不等式解集的过程,借助一元二次方程的求根公式,直接写出关于x的不等式ax2+bx+c>0(a>0)的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
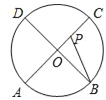
【题目】如图:点A、B、C、D为⊙O上的四等分点,动点P从圆心O出发,沿O﹣C﹣D﹣O的路线做匀速运动.设运动的时间为t秒,∠APB的度数为y.则下列图象中表示y与t之间函数关系最恰当的是( )
A. 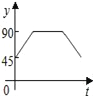 B.
B.  C.
C. 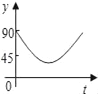 D.
D. 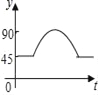
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)求该抛物线的解析式.
(2)一动点P在(1)中抛物线上滑动且满足S△ABP=10,求此时P点的坐标.
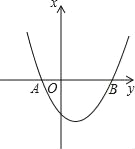
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2﹣2x﹣3与x轴交于点A、B(3,0),交y轴于点C
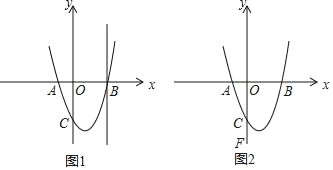
(1)求a的值.
(2)过点B的直线1与(1)中的抛物线有且只有一个公共点,则直线1的解析式为 .
(3)如图2,已知F(0,﹣7),过点F的直线m:y=kx﹣7与抛物线y=x2﹣2x﹣3交于M、N两点,当S△CMN=4时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】码头工人每天往一艘轮船50吨货物,装载完毕恰好用了8天时间.
(1)轮船到达目的地后开始卸货,平均卸货速度v(单位:吨/天)与卸货时间t(单位:天)之间有怎样的函数关系?
(2)由于遇到紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸多少吨货物?
(3)若原有码头工人10名,在(2)的条件下,至少需要增加多少名工人才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
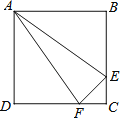
【题目】如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
A. 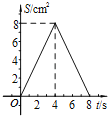 B.
B. 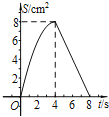
C. 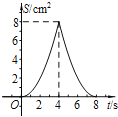 D.
D. 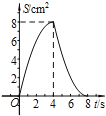
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com