
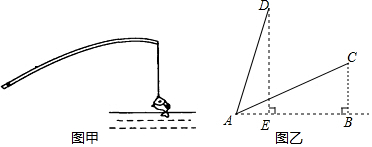
分析 Rt△ABC中由AC=6、BC=3得AB=3$\sqrt{2}$、∠BAC=30°,从而知∠DAE=75°、∠D=15°,作AD的垂直平分线交AD于点F,交DE于点G,可得∠AGE=30°,设AE=x、AG=DG=2x,知GE=$\sqrt{3}$x、DE=(2+$\sqrt{3}$)x,Rt△ADE中,由AE2+DE2=AD2可得x的值,继而可得答案.
解答 解:如图,在Rt△ABC中,
∵AC=6、BC=3,
∴AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{2}$,∠BAC=30°,
∵∠DAC=45°,
∴∠DAE=75°,∠D=15°,
作AD的垂直平分线交AD于点F,交DE于点G,
则∠D=∠DAG=15°,DG=AG,
∴∠AGE=30°,
设AE=x,则AG=DG=2x,
∴GE=AGcos∠AGE=2x•$\frac{\sqrt{3}}{2}$=$\sqrt{3}$x,
∴DE=DG+EG=2x+$\sqrt{3}$x=(2+$\sqrt{3}$)x,
在Rt△ADE中,由AE2+DE2=AD2可得x2+[(2+$\sqrt{3}$)x]2=62,
解得:x=$\frac{3}{2}$($\sqrt{6}$-$\sqrt{2}$)或x=-$\frac{3}{2}$($\sqrt{6}$-$\sqrt{2}$)(舍),
即AE=$\frac{3}{2}$($\sqrt{6}$-$\sqrt{2}$),
∴BE=AB-AE=3$\sqrt{3}$-$\frac{3}{2}$($\sqrt{6}$-$\sqrt{2}$)=$\frac{6\sqrt{3}-3\sqrt{6}+3\sqrt{2}}{2}$.
点评 本题主要考查解直角三角形的应用,通过作中垂线将15度角转化为30度的特殊角求解是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直线y=$-\frac{1}{2}$x+2交坐标轴于A、B两点,C为线段OA上一点,AC=BC,AD⊥AB,BD平分∠OBC,反比例函数y=$\frac{k}{x}$的图象经过点D,则k=-8.
如图,直线y=$-\frac{1}{2}$x+2交坐标轴于A、B两点,C为线段OA上一点,AC=BC,AD⊥AB,BD平分∠OBC,反比例函数y=$\frac{k}{x}$的图象经过点D,则k=-8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com