分析:①先找出方程mx2-14x-7=0中的a,b及c的值,利用根与系数关系求出两根之和与两根之积,代入所求的代数式中化简可得;
②利用因式分解的方法求出方程y2-2(n+1)y+n2+2n=0的两解,根据两解y1与y2的范围,确定出y1与y2的值,代入所求的代数式可用n表示出来,且根据y1与y2的范围列出不等式,可得n的范围;
③由方程mx2-14x-7=0有解,可得根的判别式大于等于0,列出关于m的不等式,求出不等式的解集可得m的范围;再由第一问和第二问所表示出式子代入所求的等式中,化简可得m与n的二次函数关系式,由自变量n的范围,根据二次函数的图象可得函数值m的范围,求出两个m范围的公共部分可得满足题意m的范围.
解答:解:①∵mx
2-14x-7=0,
∴a=m,b=-14,c=-7,
∴x
1+x
2=-
=
,x
1x
2=-
,
则
-=
+
=m;
②∵方程y
2-2(n+1)y+n
2+2n=0有两个实数根,则△=4(n+1)
2-4(n
2+2n)=4>0,
分解因式得,[y-(n+2)](y-n)=0,
∴y
1=n,y
2=n+2,
∴2(2y
1-y
22)+14=2[2n-(n+2)
2]+14=-2n
2-4n+6,
∵-2≤y
1<y
2≤4,
∴-2≤n<n+2≤4,
解得:-2≤n≤2;
③∵方程mx
2-14x-7=0有两个实数根,则△=196+28m≥0,
∴m≥-7,且m≠0,(i)
∵x
1+x
2=
,x
1x
2=-
,
由①得y
1=n-2,y
2=n,
所以
-=2(2y
1-y
22)+14变形为
+
=2[2n-(n+2)
2]+14,
化简得,m=-2n
2-4n+6.
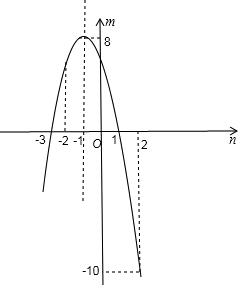
画出m关于n的二次函数图象,如图所示:
由二次函数的图象知,
当-2≤n≤2时,-10≤m≤8,(ii)
由(i)和(ii)得:-7≤m≤8且m≠0.
点评:此题考查了根与系数的关系,解字母系数的一元二次方程,以及二次函数的图象与性质,学生在利用根与系数关系时,前提必须方程有解(b
2-4ac≥0),然后可得x
1+x
2=-
,x
1x
2=
,本题的难点是第三问求m的范围,方法是根据m与n成二次函数关系,由自变量n的范围,借助二次函数的图象,利用数形结合的思想,观察图象可得函数值m在自变量n范围中所对应的最值,进而得到m的范围.




 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案