
 已知,如图,PA是⊙O切线,切点为A,PB交⊙O于C且过圆心O,D是OB中点,连结AB并延长交⊙O于E,若∠APB=30°,AP=$\sqrt{6}$,求AE的长.
已知,如图,PA是⊙O切线,切点为A,PB交⊙O于C且过圆心O,D是OB中点,连结AB并延长交⊙O于E,若∠APB=30°,AP=$\sqrt{6}$,求AE的长. 分析 过A作AH⊥BC于H,连接AO,利用三角函数求得AH=$\frac{1}{2}$AP=$\frac{\sqrt{6}}{2}$,由于PA是⊙O切线,得到AO⊥PA,解直角三角形的AO=$\sqrt{2}$,根据同圆的半径相等得到OD=OB=$\sqrt{2}$,由于D是OB中点,得到OD=BD=$\frac{1}{2}$OB=$\frac{\sqrt{2}}{2}$,CD=$\frac{3\sqrt{2}}{2}$,在RtAHO中,OH=$\sqrt{A{O}^{2}-A{H}^{2}}$=$\frac{\sqrt{2}}{2}$,在RtAHD中,AD=$\sqrt{A{H}^{2}+D{H}^{2}}$=$\frac{\sqrt{14}}{2}$,根据相交弦定理得到比例式AD•DE=CD•DB,于是求得结论.
解答 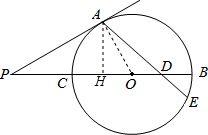 解:如图,过A作AH⊥BC于H,连接AO,
解:如图,过A作AH⊥BC于H,连接AO,
∵∠APB=30°,AP=$\sqrt{6}$,
∴AH=$\frac{1}{2}$,AP=$\frac{\sqrt{6}}{2}$,
∵PA是⊙O切线,
∴AO⊥PA,
∴AO=$\sqrt{2}$,
∴OD=OB=$\sqrt{2}$,
∵D是OB中点,
∴OD=BD=$\frac{1}{2}$OB=$\frac{\sqrt{2}}{2}$,
∴CD=$\frac{3\sqrt{2}}{2}$,
在RtAHO中,OH=$\sqrt{A{O}^{2}-A{H}^{2}}$=$\frac{\sqrt{2}}{2}$,
在RtAHD中,AD=$\sqrt{A{H}^{2}+D{H}^{2}}$=$\frac{\sqrt{14}}{2}$,
∵AD•DE=CD•DB,
∴DE=$\frac{3\sqrt{14}}{14}$,
∴AE=AD+DE=$\frac{5\sqrt{14}}{7}$.
点评 本题考查了切线的性质,解直角三角形,相交弦定理,过A作AH⊥BC,构造直角三角形是解题的关键.


科目:初中数学 来源: 题型:选择题
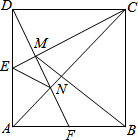 如图,正方形ABCD中,E为AD的中点,DF⊥CE于M,交AC于N,交AB于F,连接EN、BM,有如下结论:①△ADF≌△DCE;②MN=FN;③BM=BC;④S△ADN:S四边形CNFB=2:5;⑤∠ADF=∠BMF.其中正确的结论有( )
如图,正方形ABCD中,E为AD的中点,DF⊥CE于M,交AC于N,交AB于F,连接EN、BM,有如下结论:①△ADF≌△DCE;②MN=FN;③BM=BC;④S△ADN:S四边形CNFB=2:5;⑤∠ADF=∠BMF.其中正确的结论有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是某商品的商标,由七个形状、大小完全相同的正六边形组成.我们称正六边形的顶点为格点,已知△ABC的顶点都在格点上,且AB边位置如图所示,则△ABC是直角三角形的个数有( )
如图是某商品的商标,由七个形状、大小完全相同的正六边形组成.我们称正六边形的顶点为格点,已知△ABC的顶点都在格点上,且AB边位置如图所示,则△ABC是直角三角形的个数有( )| A. | 6个 | B. | 8个 | C. | 10个 | D. | 12个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 2 | 2 | 4 | 3 | 3 | 2 |
| A. | 4 | B. | 1.75 | C. | 1.70 | D. | 1.65 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
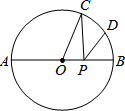 如图,已知⊙O的半径为R,C、D是直径AB的同侧圆周上的两点,弧AC的度数为100°弧BC=2弧BD,动点P在线段AB上,则PC+PD的最小值为( )
如图,已知⊙O的半径为R,C、D是直径AB的同侧圆周上的两点,弧AC的度数为100°弧BC=2弧BD,动点P在线段AB上,则PC+PD的最小值为( )| A. | R | B. | $\sqrt{2}$R | C. | $\sqrt{3}$R | D. | $\frac{\sqrt{5}}{2}$R |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com