
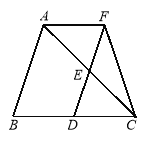
【题目】如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接CF.
(1)求证:四边形ABDF是平行四边形;
(2)若∠CAF=45°,BC=4,CF=![]() ,求△CAF的面积.
,求△CAF的面积.
【答案】(1)证明见解析;(2)3.
【解析】
试题分析:(1)根据平行四边形的定义即可证得.
(2)由平行四边形的性质得AF=BD=2,过点F作FG⊥AC于G点,从而由等腰直角三角形的性质得AG=GF=![]() ,在Rt△FGC中应用勾股定理求得GC的长,即可得AC=AG+GC=
,在Rt△FGC中应用勾股定理求得GC的长,即可得AC=AG+GC=![]() ,从而求得△CAF的面积.
,从而求得△CAF的面积.
试题解析:(1)∵点D、E分别是边BC、AC的中点,∴DE∥AB.
∵AF∥BC,
∴四边形ABDF是平行四边形.
(2)如图,过点F作FG⊥AC于G点.
∵BC=4,点D是边BC的中点,∴BD=2.
由(1)可知四边形ABDF是平行四边形,∴AF=BD=2.
∵∠CAF=45°,∴AG=GF=![]() .
.
在Rt△FGC中,∠FGC=90°, GF=![]() ,CF=
,CF=![]() ,
,
∴GC=![]() .
.
∴AC=AG+GC=![]() .
.
∴![]() .
.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】把所有正偶数从小到大排列,并按如下规律分组:(2)、(4,6),(8,10,12),(14,16,18,20),…,现有等式Am=(i,j)表示正偶数m是第i组第j个数(从左往右数).如A2=(1,1),A10=(3,2),A18=(4,3),则A200可表示为( )
A.(14,9)B.(14,10)C.(15,9)D.(15,10)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是学校的大门,教师的办公室A位于点O的北偏东45°,学生宿舍B位于点O的南偏东30°,
(1)请在图中画出射线OA、射线OB,并计算∠AOB的度数;
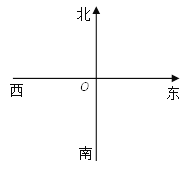
(2)七年级教室C在∠AOB的角平分线上,画出射线OC,并通过计算说明七年级教室相对于点O的方位角.
查看答案和解析>>
科目:初中数学 来源: 题型:
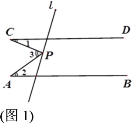
【题目】已知直线AB∥CD,点P为直线l上一点,尝试探究并解答:
(1)如图1,若点P在两平行线之间,∠1=23°,∠2=35°,则∠3= ;
(2)探究图1中∠1,∠2与∠3之间的数量关系,并说明理由;
(3)如图2,若点P在CD的上方,探究∠1,∠2与∠3之间有怎样的数量关系,并说明理由;
(4)如图3,若∠PCD与∠PAB的平分线交于点P1,∠DCP1与∠BAP1的平分线交于点P2,∠DCP2与∠BAP2的平分线交于点P3,…,∠DCPn-1与∠BAPn-1的平分线交于点Pn,若∠PCD=α,∠PAB=β,直接写出∠APnC的度数(用含α与β的代数式表示).


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在关系式![]() 中有下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④用关系式表示的不能用图像表示;⑤y与x的关系还可以用列表法和图像法表示,其中说法正确的是( ).
中有下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④用关系式表示的不能用图像表示;⑤y与x的关系还可以用列表法和图像法表示,其中说法正确的是( ).
A.①②⑤B.①②④C.①③⑤D.①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB = 6cm,∠CAB = 25°,P是线段AB上一动点,过点P作PM⊥AB交射线AC于点M,连接MB,过点P作PN⊥MB于点N.设A,P两点间的距离为xcm,P,N两点间的距离为ycm.(当点P与点A或点B重合时,y的值均为0)小海根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.

下面是小海的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0.00 | 0.60 | 1.00 | 1.51 | 2.00 | 2.75 | 3.00 | 3.50 | 4.00 | 4.29 | 4.90 | 5.50 | 6.00 |
y/cm | 0.00 | 0.29 | 0.47 | 0.70 | 1.20 | 1.27 | 1.37 | 1.36 | 1.30 | <>1.00 | 0.49 | 0.00 |
(说明:补全表格时相关数值保留两位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:当y=0.5时,与之对应的![]() 值的个数是 .
值的个数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
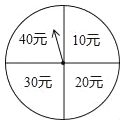
【题目】端午节期间,扬州某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成4个面积相等的扇形,四个扇形区域里分别标有“10元”、“20元”、“30元”、“40元”的字样(如图).规定:同一日内,顾客在本商场每消费满100元就可以转动转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券,某顾客当天消费240元,转了两次转盘.
(1)该顾客最少可得 元购物券,最多可得 元购物券;
(2)请用画树状图或列表的方法,求该顾客所获购物券金额不低于50元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com