
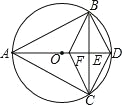
【题目】如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=8,AD=10,求CD的长.
【答案】(1)证明见解析;(2)四边形BFCD是菱形.证明见解析;(3)![]() .
.
【解析】
试题分析:(1)证明△ABD≌△ACD,得到∠BAD=∠CAD,根据等腰三角形的性质即可证明;
(2)菱形,证明△BFE≌△CDE,得到BF=DC,可知四边形BFCD是平行四边形,易证BD=CD,可证明结论;
(3)设DE=x,则根据CE2=DEAE列方程求出DE,再用勾股定理求出CD.
试题解析:(1)∵AD是直径,
∴∠ABD=∠ACD=90°,
在Rt△ABD和Rt△ACD中,
![]() ,
,
∴Rt△ABD≌Rt△ACD,
∴∠BAD=∠CAD,
∵AB=AC,
∴BE=CE;
(2)四边形BFCD是菱形.
证明:∵AD是直径,AB=AC,
∴AD⊥BC,BE=CE,
∵CF∥BD,
∴∠FCE=∠DBE,
在△BED和△CEF中
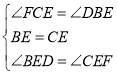 ,
,
∴△BED≌△CEF,
∴CF=BD,
∴四边形BFCD是平行四边形,
∵∠BAD=∠CAD,
∴BD=CD,
∴四边形BFCD是菱形;
(3)∵AD是直径,AD⊥BC,BE=CE,
∴CE2=DEAE,
设DE=x,
∵BC=8,AD=10,
∴42=x(10-x),
解得:x=2或x=8(舍去)
在Rt△CED中,
CD=![]() .
.


科目:初中数学 来源: 题型:
【题目】改写命题“平行于同一直线的两直线平行”:如果___________________________,
那么___________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励创业,市政府制定了小型企业的优惠政策,许多小型企业应运而生,我县统计了2015年1-5月新注册小型企业的数量,并将结果绘制成如图所示两种不完整的统计图:

(1)我县2015年1-5月新注册小型企业一共有 家.扇形统计图中“2月”所在扇形的圆心角为 度;
(2) 请将折线统计图补充完整;
(3)在2015年3月新注册的小型企业中,只有2家是餐饮企业,现从3月新注册的小型企业中随机抽取2家企业了解其经营状况,请用列表或画树状图的方法求出所抽取的2家企业恰好都是餐饮企业的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
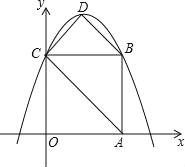
【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A、C分别在x轴、y轴的正半轴,抛物线y=-![]() x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.
x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米且垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( )

A.(6+![]() )米 B.12米
)米 B.12米
C.(4-2![]() )米 D.10米
)米 D.10米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程a(1+x2)+2bx=c(1-x2),其中a、b、c分别为△ABC三边的长,如果方程有两个相等的实数根,则△ABC的形状为( )
A. 等腰三角形
B. 等边三角形
C. 直角三角形
D. 等腰直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com