
 如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为3,6或6.5或5.4时,△ACP是等腰三角形.
如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为3,6或6.5或5.4时,△ACP是等腰三角形. 分析 根据题意分四种情况,针对每种情况画出相应的图形,求出相应的时间t的值即可解答本题.
解答  解:由题意可得,
解:由题意可得,
第一种情况:当AC=CP时,△ACP是等腰三角形,如右图1所示,
∵在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,
∴CP=6cm,
∴t=6÷2=3秒;
第二种情况:当CP=PA时,△ACP是等腰三角形,如右图2所示,
∵在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,
∴AB=10cm,∠PAC=∠PCA,
∴∠PCB=∠PBC,
∴PA=PC=PB=5cm,
∴t=(CB+BP)÷2=(8+5)÷2=6.5秒;
第三种情况:当AC=AP时,△ACP是等腰三角形,如右图3所示,
∵在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,
∴AP=6cm,AB=10cm,
∴t=(CB+BA-AP)÷2=(8+10-6)÷2=6秒;
第四种情况:当AC=CP时,△ACP是等腰三角形,如右图4所示,
作CD⊥AB于点D,
∵∠ACB=90°,AC=6cm,BC=8cm,tan∠A=$\frac{BC}{AC}=\frac{8}{6}$=$\frac{CD}{AD}$,
∴$\frac{CD}{AD}=\frac{4}{3}$,AB=10cm,
设CD=4a,则AD=3a,
∴(4a)2+(3a)2=62,
解得,a=$\frac{6}{5}$,
∴AD=3a=$\frac{18}{5}$,
∴AP=2AD=7.2cm,
∴t=$\frac{8+10-7.2}{2}$=5.4s,
故答案为:3,6或6.5或5.4.
点评 本题考查等腰三角形的判定,解题的关键是明确题意,利用分类讨论的数学思想解答问题.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:解答题
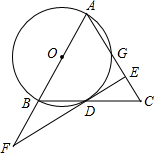 如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC边于边D,交AC边于点G,过D作⊙O的切线EF,交AB的延长线于点F,交AC于点E.
如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC边于边D,交AC边于点G,过D作⊙O的切线EF,交AB的延长线于点F,交AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知线段AB=18米,MA⊥AB于点A,MA=6米,射线BD⊥AB于B,P点从B点向A运动,每秒走1米,Q点从B点向D运动,每秒走2米,P、Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )
如图,已知线段AB=18米,MA⊥AB于点A,MA=6米,射线BD⊥AB于B,P点从B点向A运动,每秒走1米,Q点从B点向D运动,每秒走2米,P、Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )| A. | 4 | B. | 6 | C. | 4或9 | D. | 6或9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,平行四边形ABCD的周长为30cm,AB≠AD,AC、BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )
如图,平行四边形ABCD的周长为30cm,AB≠AD,AC、BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )| A. | 10cm | B. | 15cm | C. | 20cm | D. | 30cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com