
 广雅中学课外活动小组准备建一个矩形花房,其中一边靠墙,另外三边用长为50米的篱笆围成.已知墙长30米(如图所示),设这个花房垂直于墙的一边AB=x米,花房中间修筑两条互相垂直的宽为2m的小路,剩余部分种植花卉,仅在BC边的小路处留有2米宽的门.
广雅中学课外活动小组准备建一个矩形花房,其中一边靠墙,另外三边用长为50米的篱笆围成.已知墙长30米(如图所示),设这个花房垂直于墙的一边AB=x米,花房中间修筑两条互相垂直的宽为2m的小路,剩余部分种植花卉,仅在BC边的小路处留有2米宽的门.分析 (1)根据题意列出函数表达式,注意在BC边的小路处留有2米宽的门这一要求;
(2)根据长方形的面积减去小路的面积,列出S与x的函数关系式;
(3)运用二次函数的性质解决最值.
解答 解:(1)y=52-2x(10≤x≤$\frac{52}{3}$);
(2)S=(x-2)(52-2x-2)=(x-2)(50-2x)=-2x2+54x-100;
(3)S=-2x2+54x-100=-2(x-13.5)2+264.5,
当垂直于墙的一边长为13.5米时,面积S有最大值,最大值是264.5平方米.
点评 本题考查的是二次函数的实际应用.正确理解“在BC边的小路处留有2米宽的门”,正确列出函数表达式是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
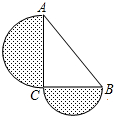 如图,在Rt△ABC中,∠C=90°,以AC、BC为直径的半圆面积分别是12.5πcm2和4.5πcm2,则Rt△ABC的面积为30cm2.
如图,在Rt△ABC中,∠C=90°,以AC、BC为直径的半圆面积分别是12.5πcm2和4.5πcm2,则Rt△ABC的面积为30cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com