
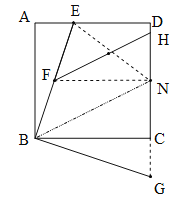
【题目】如图,正方形ABCD中,DE=2AE=4, F是BE的中点,点H在CD上,∠EFH=45°,则FH的长度为________.

【答案】![]()
【解析】过B作BN∥FG交DC于G,连接EN.把△ABE绕B顺时针旋转90°得到△BCH.
由BN∥FG,得到∠EBN=∠EFH=45°,故∠ABE+∠NBC=45°.
由旋转的性质得到△ABE≌△CBG,进而得到∠ABE=∠CBG,BE=BG,AE=CG,得到∠EBN=∠GBN.从而可以证明△EBN≌△GBN,得到EN=NG.
设NC=x,则EN=NG=x+2,DN=6-x.在Rt△EDN中,用勾股定理得到x=3, DN=NC,由EF=FB,得到FN是梯形EBCD的中位线,由梯形中位线定理得到FN的长.
通过证明△FHN∽△BNC,得到HN的长.在Rt△FNH中,由勾股定理即可得到结论.
过B作BN∥FG交DC于G,连接EN.把△ABE绕B顺时针旋转90°得到△BCH.
∵正方形ABCD中,DE=2AE=4,∴AE=2,∴AB=BC=CD=DA=6.
∵∠EFH=45°,BN∥FG,∴∠EBN=∠EFH=45°,∴∠ABE+∠NBC=45°.
∵△ABE≌△CBG,∴∠ABE=∠CBG,BE=BG,AE=CG,∴∠NBG=45°,∴∠EBN=∠GBN.
在△EBN和△GBN中,∵BE=BG,∠EBN=∠GBN,BN=BN,∴△EBN≌△GBN,∴EN=NG.
设NC=x,则EN=NG=x+2,DN=6-x.在Rt△EDN中,∵![]() ,∴
,∴![]() ,解得:x=3,∴DN=NC.
,解得:x=3,∴DN=NC.
∵EF=FB,∴FN是梯形EBCD的中位线,∴FN=(ED+BC)÷2=(4+6)÷2=5.
∵FH∥BN,∴∠FHN=∠BNC.
∵FN∥BC,∴∠FNH=∠BCN=90°,∴△FHN∽△BNC,∴FN:BC=HN:NC,∴5:6=HN:3,∴HN=2.5,∴FH=![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】已知O为圆锥的顶点,M为圆锥底面上一点,点P在OM上.一只蜗牛从P点出发,绕圆锥侧面爬行,回到P点时所爬过的最短路线的痕迹如图所示.若沿OM将圆锥侧面剪开并展开,所得侧面展开图是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,中途与乙相遇后休息了一会儿,然后以原来的速度继续行驶直到A地.设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示,则乙车到达A地时甲车距B地的路程为___________ 千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
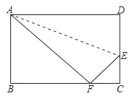
【题目】如图已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
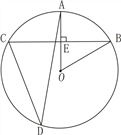
【题目】如图,在⊙O 中,BC是弦,OA⊥BC于点E,D为⊙O上一点,连接AD,CD.
(1)求证:∠AOB=2∠ADC;
(2)若OB⊥CD,CD=8,OE=![]() ,求tan∠ADC.
,求tan∠ADC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区举行“中华诵![]() 经典诵读”大赛,小学、中学组根据初赛成绩,各选出5名选手组成小学代表队和中学代表队参加市级决赛,两个代表队各选出的5名选手的决赛成绩分别绘制成下列两个统计图
经典诵读”大赛,小学、中学组根据初赛成绩,各选出5名选手组成小学代表队和中学代表队参加市级决赛,两个代表队各选出的5名选手的决赛成绩分别绘制成下列两个统计图

根据以上信息,整理分析数据如下:
平均数(分 | 中位数(分 | 众数(分 | |
小学组 | 85 |
| 100 |
中学组 |
| 85 |
|
(1)写出表格中![]() ,
,![]() ,
,![]() 的值:
的值:![]() ,
,![]() ,
,![]() .
.
(2)结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面表格是某次篮球联赛部分球队不完整的积分表:
队名 | 比赛场数 | 胜场 | 负场 | 积分 |
前进 | 14 | 10 | 4 | 24 |
光明 | 14 | 9 | 5 | 23 |
远大 | 14 |
|
| 22 |
卫星 | 14 | 4 | 10 |
|
钢铁 | 14 | 0 | 14 | 14 |
请根据表格提供的信息:
(1)求出![]() 的值;
的值;
(2)请直接写出![]() ______,
______,![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
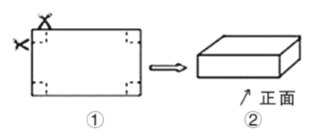
【题目】如图①是一张长为18![]() ,宽为12
,宽为12![]() 的长方形硬纸板,把它的四个角都剪去一个边长为
的长方形硬纸板,把它的四个角都剪去一个边长为![]() 的小正方形,然后把它折成一个无盖的长方体盒子(如图②),请回答下列问题:
的小正方形,然后把它折成一个无盖的长方体盒子(如图②),请回答下列问题:
(1)折成的无盖长方体盒子的容积![]()
![]() ;(用含
;(用含![]() 的代数式表示即可,不需化简)
的代数式表示即可,不需化简)
(2)请完成下表,并根据表格回答,当![]() 取什么正整数时,长方体盒子的容积最大?
取什么正整数时,长方体盒子的容积最大?
| 1 | 2 | 3 | 4 | 5 |
| 160 | ________ | 216 | ________ | 80 |
(3)从正面看折成的长方体盒子,它的形状可能是正方形吗?如果是正方形,求出![]() 的值;如果不是正方形,请说明理由.
的值;如果不是正方形,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com