【题目】晚上，小亮走在大街上．他发现：当他站在大街两边的两盏路灯之间，并且自己被两边路灯照在地上的两个影子成一直线时，自己右边的影子长为3米，左边的影子长为1．5米．又知自己身高1．80米，两盏路灯的高相同，两盏路灯之间的距离为12米，则路灯的高为 米．
【答案】6．6．
【解析】试题分析：本题是压轴题；转化思想．考查相似三角形的判定与性质的实际应用及分析问题、解决问题的能力．利用数学知识解决实际问题是中学数学的重要内容．解决此问题的关键在于正确理解题意的基础上建立数学模型，把实际问题转化为数学问题．首先根据已知条件求证出△FHG∽△FDE，然后根据相似三角形的性质求得两个相似三角形的相似比，进而求出路灯DE的高度．
解：设小亮离右边的路灯为xm，则离左边的路灯为（12﹣x）m，
再设路灯的高为hm，又易证△FHG∽△FDE，△CHG∽△CBA，则
∴
=
，
=
即1．8：h=1．5：（1．5+x）；
1．8：h=3：（3+12﹣x）
求得x=4 h=6．6
即路灯高6．6米．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】在正三角系，正方形，正五边形，正六边形这几个图形中，单独选用一种图形不能进行平面镶嵌的图形是（ ）
A.正三角形 B.正方形 C.正五边形 D.正六边形
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,某市对位于笔直公路AC上两个小区A,B的供水路线进行优化改造,供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A,B之间的距离为300(
+1)米,求供水站M分别到小区A,B的距离.(结果可保留根号)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,某人在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i为1∶
,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.则A,B两点间的距离是( )
A. 15米 B. 20
米 C. 20
米 D. 10
米
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,一楼房AB后有一假山,其坡度为i=1∶
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高度.(注:坡度i是指坡面的铅直高度与水平宽度的比)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,海中两个灯塔A,B,其中B位于A的正东方向上,渔船跟踪鱼群由西向东航行,在点C处测得灯塔A在西北方向上,灯塔B在北偏东30°方向上,渔船不改变航向继续向东航行30海里到达点D,这时测得灯塔A在北偏西60°方向上,求灯塔A,B间的距离.(计算结果用根号表示,不取近似值)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】解不等式组：
，并把它的解集在数轴上表示出来．
【答案】﹣1＜x≤2，数轴表示见解析.
【解析】试题分析：分别求出不等式组中两个不等式的解集，再求出其公共解集，然后在数轴上表示出其解集.
由①得，x≤2，
由②得，x＞﹣1，
故此不等式组的解集为：﹣1＜x≤2．
在数轴上表示为：
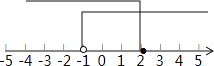
点睛: 本题考查了一元一次不等式组的解法及解集的数轴表示，先分别解两个不等式，求出它们的解集，再求两个不等式解集的公共部分.不等式组解集的确定方法是：同大取大，同小取小，大小小大取中间，大大小小无解.在数轴上空心圈表示不包含该点，实心点表示包含该点.
【题型】解答题
【结束】
22
【题目】解不等式组：
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ABC=90°，BC=3，D为AC延长线上一点，AC=3CD，过点D作DH∥AB，交BC的延长线于点H.
(1)求BD·cos∠HBD的值；
(2)若∠CBD=∠A，求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com