
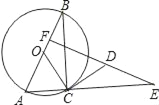
【题目】如图,⊙O是Rt△ABC的外接圆,AB为直径,∠ABC=30°,CD是⊙O的切线,E为AC延长线上一点,ED⊥AB于F.
(1)判断△DCE的形状;
(2)设⊙O的半径为1,且OF=![]() ,求证:△DCE≌△OCB.
,求证:△DCE≌△OCB.
【答案】(1)△CDE为等腰三角形;(2)证明见解析.
【解析】试题分析:(1)由∠ABC=30°可得∠BAC=60°,结合DE⊥AB,可得∠AED的度数;根据弦切角定理可得∠DCB=60°,再结合∠ACB=90°,从而可得∠DCE的度数;
(2)由(1)的证明过程可得∠ABC=∠OCB=∠DCE=∠CED=30°,要证明△BOC≌△EDC,只要证明BC=CE,接下来由圆半径为1可得AB的长,结合含30度角直角三角形的性质以及勾股定理可得AC、BC的长,在Rt△AEF中,先求得AF的长,再利用含30度角直角三角形的性质可得AE的长,继而得到CE的长,从而可证△CDE≌△COB..
(1)解:∵∠ABC=30°,
∴∠BAC=60°.
又∵OA=OC,
∴△AOC是正三角形.
又∵CD是切线,
∴∠OCD=90°.
∴∠DCE=180°﹣60°﹣90°=30°.
而ED⊥AB于F,
∴∠CED=90°﹣∠BAC=30°.
故△CDE为等腰三角形.
(2)证明:∵CD是⊙O的切线,
∴∠OCD=90°,
∵∠BAC=60°,AO=CO,
∴∠OCA=60°,∵∠DCE=30°.
∴A,C,E三点同线
在△ABC中,
∵AB=2,AC=AO=1,
∴BC=![]() =
=![]() .
.
∵OF=![]() ,
,
∴AF=AO+OF=![]() .
.
又∵∠AEF=30°,
∴AE=2AF=![]() +1,
+1,
∴CE=AE﹣AC=![]() =BC,
=BC,
而∠OCB=∠ACB﹣∠ACO=90°﹣60°=30°=∠ABC;
故△CDE≌△COB.


科目:初中数学 来源: 题型:
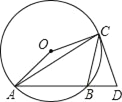
【题目】如图,点A、B、C均在⊙O上,过点C作⊙O的切线交AB的延长线于点D,∠ACB=45°,∠AOC=150°.
(1)求证:CD=CB;
(2)⊙O的半径为![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
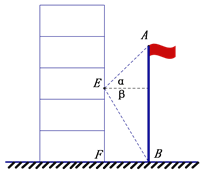
【题目】数学实践课上,同学们分组测量教学楼前国旗杆的高度.小泽同学所在的组先设计了测量方案,然后开始测量了.他们全组分成两个测量队,分别负责室内测量和室外测量(如图).室内测量组来到教室内窗台旁,在点E处测得旗杆顶部A的仰角α为45°,旗杆底部B的俯角β为60°. 室外测量组测得BF的长度为5米.则旗杆AB=______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,该店采取了降价措施.在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价4元,则平均每天销售数量为 件;
(2)当每件商品降价多少元时,该商店每天销售利润为1050元?
查看答案和解析>>
科目:初中数学 来源: 题型:
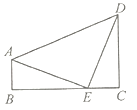
【题目】1876年,美国总统Garfield用如图所示的两个全等的直角三角形证明了勾股定理,若图中![]() ,
,![]() ,
,![]() ,则下面结论错误的是( )
,则下面结论错误的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() 是等腰直角三角形
是等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区为了绿化小区环境,建设和谐家园,准备将一块周长为76米的长方形空地,设计成长和宽分别相等的9块小长方形,如图所示,计划在空地上种上各种花卉,经市场预测,绿化每平方米空地造价210元,请计算,要完成这块绿化工程,预计花费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里有1个红球,1个黄球和n个白球,它们除颜色外其余都相同.
(1)从这个袋子里摸出一个球,记录其颜色,然后放回,摇均匀后,重复该实验,经过大量实验后,发现摸到白球的频率稳定于0.5左右,求n的值;
(2)在(1)的条件下,先从这个袋中摸出一个球,记录其颜色,放回,摇均匀后,再从袋中摸出一个球,记录其颜色.请用画树状图或者列表的方法,求出先后两次摸出不同颜色的两个球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
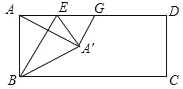
【题目】如图,矩形ABCD中,AB=3,AD=9,设AE=x.将△ABE沿BE翻折得到△ABE,点A落在矩形ABCD的内部,且∠AA′G=90°,若以点A'、G、C为顶点的三角形是直角三角形,求x的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
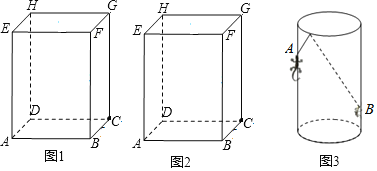
【题目】(1)如图1,长方体的长为4cm,宽为3cm,高为12cm.求该长方体中能放入木棒的最大长度;
(2)如图2,长方体的长为4cm,宽为3cm,高为12cm.现有一只蚂蚁从点A处沿长方体的表面爬到点G处,求它爬行的最短路程.
(3)若将题中的长方体换成透明圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处.求蚂蚁吃到饭粒需要爬行的最短路程是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com