
【题目】如图,边长为2的正方形ABCD内接于⊙O,过点D作⊙O的切线交BA延长线于点E,连接EO,交AD于点F,则EF长为 . 
【答案】![]()
【解析】解:连接OD,作OH⊥AD于H,

∵正方形ABCD内接于⊙O,
∴OD平分∠ADC,即∠ADO=45°,
∴△OHD为等腰直角三角形,
∴OH=DH,
∵OH⊥AD,
∴AH=DH=OH=1,
∵DE为切线,
∴OD⊥DE,
∴∠EDA=45°,
∴△EAD为等腰直角三角形,
∴AE=AD=2,
∵AE∥OH,
∴△AEF∽△HOF,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴AF= ![]() AH=
AH= ![]() ,
,
在Rt△AEF中,EF= ![]() =
= ![]() .
.
所以答案是 ![]() .
.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握正方形的性质(正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形)的相关知识才是答题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】若将30°、45°、60°的三角函数值填入表中,则从表中任意取一个值,是 ![]() 的概率为( )
的概率为( )
α | 30° | 45° | 60° |
sinα | |||
cosα | |||
tanα |
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有A,B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字.现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y).
(1)请用列表或画树状图的方法写出所有可能得到的点P的坐标;
(2)计算点P在函数y= ![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则tan∠ECF=( )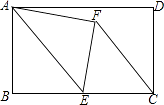
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)平面直角坐标系中,点P(x,y)的横坐标x的绝对值表示为|x|,纵坐标y的绝对值表示为|y|,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为[P],即[P]=|x|+|y|(其中的“+”是四则运算中的加法),例如点P(1,2)的勾股值[P]=|1|+|2|=3.
(1)求点A(![]() ,
, ![]() )的勾股值[A],
)的勾股值[A],
(2)若将点A向上平移3个单位,再向左平移2个单位后得到点B,请直接写出点B的坐标,并求出点B的勾股值 [B];
(3)若点M在x轴的上方,其横,纵坐标均为整数,且[M]=3,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
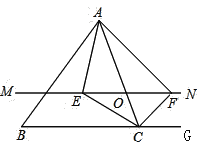
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 边上的一个动点,过点
边上的一个动点,过点![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的角平分线于点
的角平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() .
.
(1)求证:![]() ;
;
(2)当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 是矩形?并证明你的结论.
是矩形?并证明你的结论.
(3)当点![]() 运动到何处,且
运动到何处,且![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是正方形?并说明理由.
是正方形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com