
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F.切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,若AC∥EF,试判断线段KG、KD、GE间的数量关系,并说明理由;
(3)在(2)的条件下,若sinE=![]() ,AK=2
,AK=2![]() ,求⊙O的半径.
,求⊙O的半径.

【答案】(1)见解析;(2)KG2=KDGE,见解析;(3)![]()
【解析】
(1)如图1,连接OG.根据切线性质及CD⊥AB,可以推出∠KGE=∠AKH=∠GKE,根据等角对等边得到KE=GE;
(2)如图2,根据平行得角相等,证明△GKD∽△EFG,列比例式可得结论;
(3)如图3所示,连接OG,OC,由(1)得KE=GE,根据sinE![]() ,设AH=3t,则AC=5t,CH=4t,列式先求t的值,再求出圆的半径.
,设AH=3t,则AC=5t,CH=4t,列式先求t的值,再求出圆的半径.
(1)如图1,连接OG.
∵EG为切线,
∴∠KGE+∠OGA=90°.
∵CD⊥AB,
∴∠AKH+∠OAG=90°.
又∵OA=OG,
∴∠OGA=∠OAG,
∴∠KGE=∠AKH=∠GKE,
∴KE=GE.
(2)KG2=KDGE.理由如下:
连接GD,如图2.
∵AC∥EF,
∴∠C=∠E.
∵∠C=∠AGD,
∴∠E=∠AGD.
∵∠GKD=∠GKD,
∴△GKD∽△EKG,
∴![]() ,
,
∴KG2=KDEK,
由(1)得:EK=GE,
∴KG2=KDGE;
(3)连接OG,OC,如图3所示,
由(1)得:KE=GE.
∵AC∥EF,
∴∠E=∠ACH.
∵sinE=sin∠ACH![]() ,
,
设AH=3t,则AC=5t,CH=4t.
∵KE=GE,AC∥EF,
∴CK=AC=5t,
∴HK=CK﹣CH=t.
在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,
即(3t)2+t2![]() ,解得:t
,解得:t![]() .
.
设⊙O半径为r.在Rt△OCH中,OC=r,OH=r﹣3t,CH=4t,
由勾股定理得:OH2+CH2=OC2,
即(r﹣3t)2+(4t)2=r2,解得:r![]() t
t![]() ,
,
答:⊙O的半径为![]() .
.





 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】我市某公司用800万元购得某种产品的生产技术后,进一步投入资金1550万元购买生产设备,进行该产品的生产加工,已知生产这种产品每件还需成本费40元.经过市场调研发现:该产品的销售单价需要定在200元到300元之间较为合理.销售单价![]() (元)与年销售量
(元)与年销售量![]() (万件)之间的变化可近似的看作是如下表所反应的一次函数:
(万件)之间的变化可近似的看作是如下表所反应的一次函数:
销售单价 | 200 | 230 | 250 |
年销售量 | 14 | 11 | 9 |
(1)请求出![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;
(2)请说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最少亏损是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
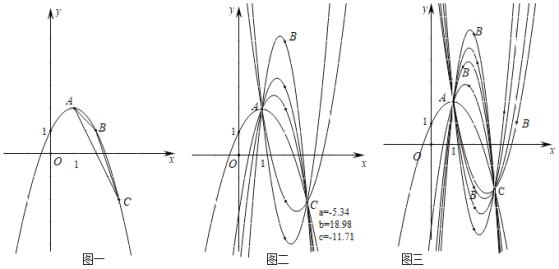
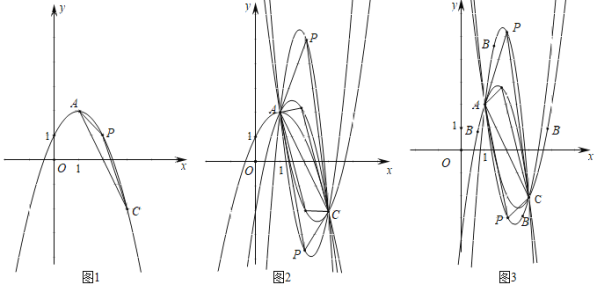
【题目】定义:连接抛物线上两点的线段叫抛物线的弦,在这两点之间抛物线上的任意一点P与此两点构成的三角形称作抛物线的弦三角,点P称作弦锥,设点P的横坐标为x.
已知抛物线经过A(1,2)、B(m,n)、C(3,﹣2)三点,P是抛物线上AC之间的一点,以AC为弦的弦三角为△PAC.
(1)图一,当m=2,n=1时,求该抛物线的解析式,若x=k1时△PAC的面积最大,求k1的值.
(2)图二,当m=2,n≠1时,用n表示该抛物线的解析式,若x=k2时△PAC的面积最大,求k2的值.k1与k2有何数量关系?
(3)图三,当m≠2,n≠1时,用m,n表示该抛物线的解析式,若x=k3时△PAC的面积最大,求k3的值.观察图1,2,3,过定点A、C,根据B在各种不同位置所得计算结果,你发现通过两个定点的抛物线系中,以此两点为弦的弦三角的面积取得最大值时,弦锥的横坐标有何规律?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一批成本为每件 30 元的商品,经调查发现,该商品每天的销售量 y(件)与销售单价 x(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量 y 与销售单价 x 之间的函数关系式;
(2)若商店按单价不低于成本价,且不高于 50 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润 w(元)最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润不低于 800 元,则每天的销售量最少应为多少件?

查看答案和解析>>
科目:初中数学 来源: 题型:
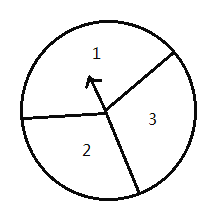
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.
(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为 ;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文明小区50平方米和80平方米两种户型的住宅,50平方米住宅套数是80平方米住宅套数的2倍.物管公司月底按每平方米2元收取当月物管费,该小区全部住宅都人住且每户均按时全额缴纳物管费.
(1)该小区每月可收取物管费90 000元,问该小区共有多少套80平方米的住宅?
(2)为建设“资源节约型社会”,该小区物管公司5月初推出活动一:“垃圾分类送礼物”,50平方米和80平方米的住户分别有40%和20%参加了此次括动.为提离大家的积扱性,6月份准备把活动一升级为活动二:“拉圾分类抵扣物管费”,同时终止活动一.经调査与测算,参加活动一的住户会全部参加活动二,参加活动二的住户会大幅增加,这样,6月份参加活动的50平方米的总户数在5月份参加活动的同户型户数的基础上将增加![]() ,每户物管费将会减少
,每户物管费将会减少![]() ;6月份参加活动的80平方米的总户数在5月份参加活动的同户型户数的基础上将增加
;6月份参加活动的80平方米的总户数在5月份参加活动的同户型户数的基础上将增加![]() ,每户物管费将会减少
,每户物管费将会减少![]() .这样,参加活动的这部分住户6月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少
.这样,参加活动的这部分住户6月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坡度i=1:![]() 的斜坡AB上立有一电线杆EF,工程师在点A处测得E的仰角为60°,沿斜坡前进20米到达B,此时测得点E的仰角为15°,现要在斜坡AB上找一点P,在P处安装一根拉绳PE来固定电线杆,以使EF保持竖直,为使拉绳PE最短,则FP的长度约为_____.(参考数据:
的斜坡AB上立有一电线杆EF,工程师在点A处测得E的仰角为60°,沿斜坡前进20米到达B,此时测得点E的仰角为15°,现要在斜坡AB上找一点P,在P处安装一根拉绳PE来固定电线杆,以使EF保持竖直,为使拉绳PE最短,则FP的长度约为_____.(参考数据:![]() =1.414,
=1.414,![]() =1.732)
=1.732)
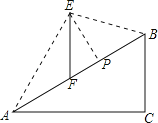
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,AB=5,BC=4,点D为边AC上的动点,作菱形DEFG,使点E、F在边AB上,点G在边BC上.若这样的菱形能作出两个,则AD的取值范围是( )
,AB=5,BC=4,点D为边AC上的动点,作菱形DEFG,使点E、F在边AB上,点G在边BC上.若这样的菱形能作出两个,则AD的取值范围是( )
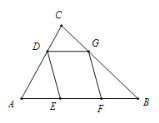
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/s秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q也同时停止运动,当点P运动__秒时,以P、Q、E、F为顶点的四边形是平行四边形.
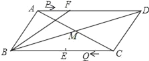
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com