
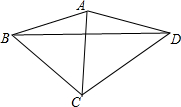
 如图,∠ABD=∠ADB=15°,∠CBD=45°,∠CDB=30°.求证:△ABC是等边三角形.
如图,∠ABD=∠ADB=15°,∠CBD=45°,∠CDB=30°.求证:△ABC是等边三角形. 分析 如图作等边三角形BDE,连结AE,先证明△ABE≌△ADE,再证明△BAE≌△BCD得到AB=BC由此即可证明.
解答 证明:如图作等边三角形BDE,连结AE.
∵∠ABD=∠ADB=15°,
∴AB=AD
∵EB=ED,
在△ABE和△ADE中,
$\left\{\begin{array}{l}{AE=AE}\\{EB=ED}\\{AB=AD}\end{array}\right.$,
∴△ABE≌△ADE(SSS),
∴∠AEB=∠AED=30°,
∵∠BDC =30°,
=30°,
∴∠AEB=∠BDC,
∵∠EBD=60°,∠ABD=15°,
∴∠EBA=45°=∠CBD
在△BAE和△BCD中,
$\left\{\begin{array}{l}{∠BEA=∠BDC}\\{BE=DB}\\{∠EBA=∠CBD}\end{array}\right.$
∴△BAE≌△BCD(ASA)
∴BA=BC
∵∠ABC=∠ABD+∠CBD
=15°+45°
=60°
∴△ABC是等边三角形.
点评 本题考查等边三角形的判定、全等三角形的判定和性质等知识,解题的关键是添加辅助线构造全等三角形,题目有点难度,记住作等边三角形也是常用辅助线,属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
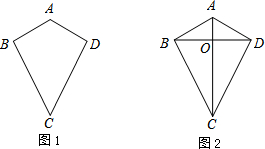
 如图,在△ABC中,∠ACB=90°,AC=BC=6,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示),那么,在上述旋转过程中:
如图,在△ABC中,∠ACB=90°,AC=BC=6,现将一块边长足够大的直角三角板的直角顶点置于AB的中点O,两直角边分别经过点B、C,然后将三角板绕点O按顺时针方向旋转一个角度α(0°<α<90°),旋转后,直角三角板的直角边分别与AC、BC相交于点K、H,四边形CHOK是旋转过程中三角板与△ABC的重叠部分(如图所示),那么,在上述旋转过程中:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com