
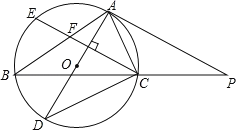
【题目】如图,AD是△ABC的外接圆⊙O的直径,点P在BC延长线上,PA是⊙O的切线,且∠B=35°.
(1)求∠PAC的度数.
(2)弦CE⊥AD交AB于点F,若AFAB=12,求AC的长.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中的点P(x,y)(x≠0),将它的纵坐标y与横坐标x的比称为点P的“湘一比”,记为kp,如点P(﹣3,6),则kp=![]() =﹣2.
=﹣2.
(1)若P(a,2)在直线y=x﹣2上,求点P的“湘一比”kp及直线OP与x轴夹角的正切值;
(2)已知点Q(m,n)的“湘一比”kQ为![]() ,且Q在y=
,且Q在y=![]() (x>0)上,⊙Q的半径为1,若点M在⊙Q上,求M的“湘一比”kM的取值范围;
(x>0)上,⊙Q的半径为1,若点M在⊙Q上,求M的“湘一比”kM的取值范围;
(3)设m、n为正整数,且m≠2,对一切实数t,如果直线y=mtx+3mt与二次函数y=x2+3x交于A(x1,y1),B(x2,y2),且|x1﹣x2|≥|2t+n|,求点N(m,n)的“湘一比”kN的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知A(2t,0),B(0,-2t),C(2t,4t)三点,其中t>0,函数![]() 的图象分别与线段BC,AC交于点P,Q.若S△PAB-S△PQB=t,则t的值为__.
的图象分别与线段BC,AC交于点P,Q.若S△PAB-S△PQB=t,则t的值为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC,∠BAC=90°,BC=5,AC=2![]() ,以A为圆心、AB为半径画圆,与边BC交于另一点D.
,以A为圆心、AB为半径画圆,与边BC交于另一点D.
(1)求BD的长;
(2)连接AD,求∠DAC的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
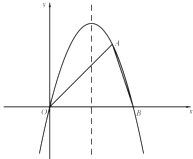
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于原点
轴交于原点![]() 和点
和点![]() ,点
,点![]() 在抛物线上.
在抛物线上.
(1)求抛物线的表达式,并写出它的对称轴;
(2)求![]() 的值;
的值;
(3)点![]() 在抛物线的对称轴上,如果
在抛物线的对称轴上,如果![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
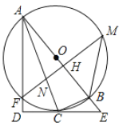
【题目】如图,![]() 为的
为的![]() 直径,
直径,![]() 为
为![]() 上一点,经过点
上一点,经过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() 交
交![]() 于
于![]() ,
,![]() 于
于![]() ,分别交
,分别交![]() 、
、![]() 于
于![]() 、
、![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:![]() 平分
平分![]() ;
;
(2)若![]() ,
,![]() ,①求
,①求![]() 的半径;②求
的半径;②求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com