
分析 (1)两边都除以2后直接开平方可得;
(2)移项后将右边化为0,再将左边提取公因式(x-3)后,解之可得;
(3)左边利用十字相乘法分解因式求解可得;
(4)直接开平方法求解可得;
(5)利用完全平方公式分解因式法求解可得;
(6)左边十字相乘法分解因式后求解可得;
(7)公式法求解可得;
(8)公式法求解可得.
解答 解:(1)∵2(x-2)2=18,
∴(x-2)2=9,
则x-2=3或x-2=-3,
解得:x=5或x=-1;
(2)∵2x(x-3)+x=3,
∴2x(x-3)+x-3=0,
∴(x-3)(2x+1)=0,
则x-3=0或2x+1=0,
解得:x=3或x=-$\frac{1}{2}$;
(3)∵x2-2x-15=0,
∴(x+3)(x-5)=0,
则x+3=0或x-5=0,
解得:x=-3或x=5;
(4)∵4(x-1)2=9(x-5)2,
∴2(x-1)=3(x-5)或2(x-1)=-3(x-5),
解得:x=13或x=$\frac{17}{5}$;
(5)∵x2-2$\sqrt{7}$x+7=0,
∴(x-$\sqrt{7}$)2=0,
∴x-$\sqrt{7}$=0,即x=$\sqrt{7}$;
(6)∵2x2-x-6=0,
∴(x-2)(2x+3)=0,
则x-2=0或2x+3=0,
解得:x=2或x=-$\frac{3}{2}$;
(7)∵a=1,b=-7,c=2,
∴△=b2-4ac=(-7)2-4×1×2=41>0,
则x=$\frac{7±\sqrt{41}}{2}$;
(8)∵a=$\frac{3}{2}$,b=-1,c=-2,
∴△=b2-4ac=(-1)2-4×$\frac{3}{2}$×(-2)=13>0,
则x=$\frac{1±\sqrt{13}}{3}$.
点评 本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两个锐角对应相等 | B. | 一个锐角、一条直角边对应相等 | ||
| C. | 两条直角边对应相等 | D. | 一条斜边、一条直角边对应相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
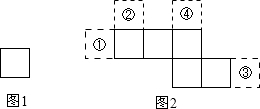
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1-10%+15%)x万元 | B. | (1+10%-15%)x万元 | C. | (1-10%)(1+15%)x万元 | D. | (x-10%)(x+15%)万元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com