
分析 (1)将原式分母有理化即可;
(2)将a分母有理化,化简为$\sqrt{2}+1$,代入①,②进行运算即可.
解答 解:(1)原式=$\frac{1}{2}$×($\sqrt{3}-1$+$\sqrt{5}$$-\sqrt{3}$+$\sqrt{7}$$-\sqrt{5}$+…+$\sqrt{121}$$-\sqrt{119}$)
=$\frac{1}{2}$×($\sqrt{121}$-1)
=$\frac{1}{2}×$10
=5;
(2)①∵a=$\sqrt{2}+1$,
∴4a2-8a+1
=4×${(\sqrt{2}+1)}^{2}$-8×($\sqrt{2}+$1)+1
=5;
②a3-3a2+a+1
=${(\sqrt{2}+1)}^{3}$-3${(\sqrt{2}+1)}^{2}$+($\sqrt{2}+1$)+1
=7+5$\sqrt{2}$-(9$+6\sqrt{2}$)+$\sqrt{2}$+1+1
=0;
2a2-5a+$\frac{1}{a}$+2
=2×${(\sqrt{2}+1)}^{2}$$-5(\sqrt{2}+1)$+$\sqrt{2}-1$+2
=2;
故答案为:0,2.
点评 本题主要考查了分母有理化,利用分母有理化化简是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 为维护南海主权,我海军舰艇加强对南海海域的巡航,2015年4月10日上午9时,我海巡001号舰艇在观察点A处观测到其正东方向80$\sqrt{2}$海里处有一灯塔S,该舰艇沿南偏东45°的方向航行,11时到达观察点B,测得灯塔S位于其北偏西15°方向,求该舰艇的巡航速度?(结果保留整数)
为维护南海主权,我海军舰艇加强对南海海域的巡航,2015年4月10日上午9时,我海巡001号舰艇在观察点A处观测到其正东方向80$\sqrt{2}$海里处有一灯塔S,该舰艇沿南偏东45°的方向航行,11时到达观察点B,测得灯塔S位于其北偏西15°方向,求该舰艇的巡航速度?(结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线BC于点D,E是AC上一点,DE=DB,以D为圆心,DC为半径作⊙D
如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线BC于点D,E是AC上一点,DE=DB,以D为圆心,DC为半径作⊙D查看答案和解析>>
科目:初中数学 来源: 题型:解答题
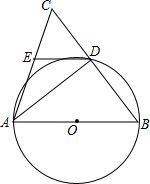 如图,在△ABC中,AB=AC,∠ABC=m°,以AB为直径的⊙O交BC于点D,连接AD.
如图,在△ABC中,AB=AC,∠ABC=m°,以AB为直径的⊙O交BC于点D,连接AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com