
 如图,矩形ABCD中,AB=6,BC=8,BC、BD上分别取点E、F,则CF+EF的最小值为7.68.
如图,矩形ABCD中,AB=6,BC=8,BC、BD上分别取点E、F,则CF+EF的最小值为7.68. 分析 根据轴对称求最短路线的方法得出F点位置,进而利用相似三角形的性质CF+EF的值.
解答 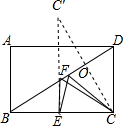 解:如图所示:由题意可得出:作C点关于BD对称点C′连接CC′,交BD于O,则CC′⊥BD,CC′=2OC,
解:如图所示:由题意可得出:作C点关于BD对称点C′连接CC′,交BD于O,则CC′⊥BD,CC′=2OC,
过点C′作C′E⊥BC于点E,交BD于点F,连接FC,此时CF+EF=C′E最小,
∵AB=6,BC=8,
∴CD=6,
∴BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=10,
∵∠COD=∠BCD=90°,∠CDO=∠BDC,
∴△COD∽△BCD,
∴$\frac{OC}{CD}$=$\frac{BC}{BD}$,即$\frac{OC}{6}$=$\frac{8}{10}$,
∴OC=4.8,
∴CC′=9.6,
∵C′E⊥BC,DC⊥BC,
∴C′E∥DC,
∴∠EC′C=∠OCD,
∴△CC′E∽△DCO,
∴$\frac{C′E}{OC}$=$\frac{CC′}{CD}$,即$\frac{C′E}{4.8}$=$\frac{9.6}{6}$,
解得C′E=7.68,
∴CF+EF的最小值为7.68.
故答案为:7.68.
点评 此题主要考查了利用轴对称求最短路线以及相似三角形的判定和性质,利用轴对称得出F点位置是解题关键.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:选择题
| A. | $-\sqrt{(-6)^{2}}=-6$ | B. | $(-\sqrt{3})^{2}=9$ | C. | $\sqrt{({-16)}^{2}}=±16$ | D. | $-(-\sqrt{\frac{16}{25}})^{2}=\frac{16}{25}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
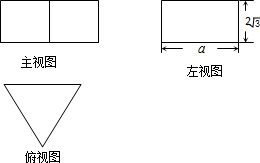 一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8$\sqrt{3}$,则a的值为( )
一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8$\sqrt{3}$,则a的值为( )| A. | $\frac{2}{3}$$\sqrt{3}$ | B. | 2+$\frac{\sqrt{3}}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
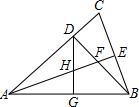 如图,△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H,下列结论错误的是( )
如图,△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H,下列结论错误的是( )| A. | AH=2DF | B. | AF=2HE | C. | AF=2CE | D. | DH=DF |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
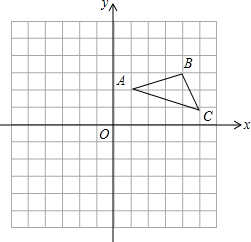 在平面直角坐标系中,△ABC的位置如图,网格中小正方形的边长为1,请解答下列问题:
在平面直角坐标系中,△ABC的位置如图,网格中小正方形的边长为1,请解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com