
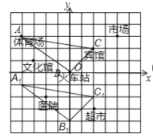
【题目】如图,这是某市部分简图,为了确定各建筑物的位置:

(1)请你以火车站为原点建立平面直角坐标系,若以小方格的边长为单位长度,写出市场的坐标为_______;超市的坐标为_____________.
(2)请将体育场为A、宾馆为C和火车站为B看作三点用线段连起来,得△ABC,然后将△ABC向下平移4个单位长度,画出平移后的![]() ,写出
,写出![]() 的坐标.
的坐标.
(3)求出![]() 的面积.
的面积.
【答案】(1)建立坐标系见解析;(4,3);(2,-3);(2)图见解析;![]() ;(3)7
;(3)7
【解析】
(1)以火车站为原点建立平面直角坐标系,然后根据平面直角坐标系即可写出结论;
(2)顺次连接体育场A、宾馆C和火车站B,可得△ABC,然后将△ABC向下平移4个单位长度,得到![]() 即可,然后根据平面直角坐标系即可写出各点坐标即可;
即可,然后根据平面直角坐标系即可写出各点坐标即可;
(3)利用长方形的面积减去3个直角三角形的面积即可求出结论.
解:(1)以火车站为原点建立平面直角坐标系,如下图所示,由平面直角坐标系可知:市场的坐标为(4,3),超市的坐标为(2,-3)
故答案为:(4,3);(2,-3);
(2)顺次连接体育场A、宾馆C和火车站B,可得△ABC,然后将△ABC向下平移4个单位长度,得到![]() ,如下图所示,
,如下图所示,![]() 即为所求,由平面直角坐标系可知:
即为所求,由平面直角坐标系可知:![]() ;
;
(3)由坐标系可得:![]() =6×3-
=6×3-![]() ×6×1-
×6×1-![]() ×4×3-
×4×3-![]() ×2×2=7
×2×2=7


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂准备翻建新的大门,厂门要求设计成轴对称的拱形曲线.已知厂门的最大宽度AB=12m,最大高度OC=4m,工厂的运输卡车的高度是3m,宽度是5.8m.现设计了两种方案.方案一:建成抛物线形状(如图1);方案二:建成圆弧形状(如图2).为确保工厂的卡车在通过厂门时更安全,你认为应采用哪种设计方案?请说明理由.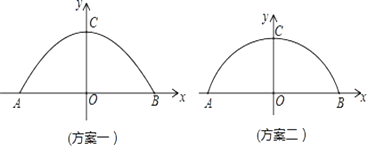
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们在学习“实数”时,画了这样一个图,以数轴上的单位长为1的线段作一个正方形,然后以原点O为圆心,正方形的对角线长为半径画弧交x轴于点A,请根据图形回答下列问题:
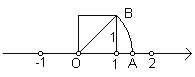
(1)线段OA的长度是___________
(2)这种研究和解决问题的方式,体现了的数学思想方法( ).
A.数形结合B.归纳C.换元D.消元
(3)计算:![]() ﹣
﹣![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于点Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
(1)求证:AF=BF;
(2)如果AB=AC,求证:四边形AFCG是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E、G、H分別在矩形ABCD的边AB、CD、DA上,AH=2.
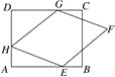
(1)已知DG=6,求AE的长;
(2)已知DG=2,求证:四边形EFGH为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B、E、C、F在一条直线上,AB=DF,AC=DE,∠A=∠D.
(1)求证:AC∥DE;
(2)若BF=13,EC=5,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是根据对初一(1)班的50名同学平时最爱吃的食物的种类进行的问卷调查绘制成的统计表,请填满缺少的项并回答后面的问题.
肉类 | 蔬菜类 | 瓜果类 | 水产类 | |
男生 | 22 | 1 | 2 | |
女生 | 4 | 5 | 3 | |
频率 | 64% | 14% | 12% |
(1)选择适当的统计图表示男生平时最爱吃的食物的种类情况;
(2)就给出的初一(1)班的同学平时最爱吃的食物的种类情况,请你结合自己的年龄特点简略谈谈自己的看法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com