
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
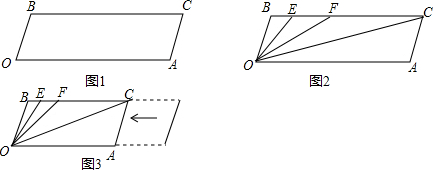
科目:初中数学 来源:2011-2012学年北京师大附中七年级下学期期中考试数学卷(带解析) 题型:解答题
已知,BC//OA,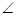 B=
B=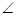 A=100°,试回答下列问题:
A=100°,试回答下列问题:
(1)如下图所示,求证:OB//AC。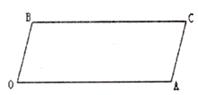
(2)如下图,若点E、F在BC上,且满足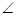 FOC=
FOC=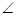 AOC,并且OE平分
AOC,并且OE平分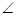 BOF。
BOF。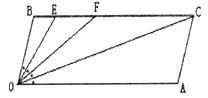
(i)求: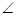 EOC的度数;
EOC的度数;
(ii)求: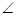 OCB:
OCB: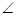 OFB的值。
OFB的值。
(iii)如下图,若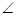 OEB=
OEB=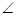 OCA,此时
OCA,此时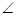 OCA度数等于 。(在横线上填上答案即可)。
OCA度数等于 。(在横线上填上答案即可)。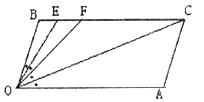
查看答案和解析>>
科目:初中数学 来源:2014届北京师大附中七年级下学期期中考试数学卷(解析版) 题型:解答题
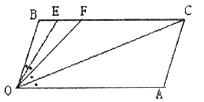
已知,BC//OA, B=
B=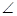 A=100°,试回答下列问题:
A=100°,试回答下列问题:
(1)如下图所示,求证:OB//AC。
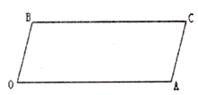
(2)如下图,若点E、F在BC上,且满足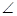 FOC=
FOC=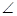 AOC,并且OE平分
AOC,并且OE平分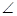 BOF。
BOF。
(i)求: EOC的度数;
EOC的度数;
(ii)求: OCB:
OCB: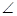 OFB的值。
OFB的值。
(iii)如下图,若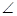 OEB=
OEB=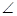 OCA,此时
OCA,此时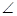 OCA度数等于
。(在横线上填上答案即可)。
OCA度数等于
。(在横线上填上答案即可)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com