
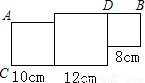
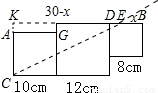
 解:如图所示,过C作直线CE交BD于点E,使三个正方形的面积分为相等的两部分,再延长KF、CA两直线相交于点K,设BE=x,
解:如图所示,过C作直线CE交BD于点E,使三个正方形的面积分为相等的两部分,再延长KF、CA两直线相交于点K,设BE=x, (30-x)×12-20=
(30-x)×12-20= (10×10+12×12+8×8),
(10×10+12×12+8×8),

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
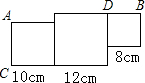 如图,由边长分别为8厘米,10厘米,12厘米的三个不同的正方形组成的图形,现请你经过C点沿一条直线把它剪开,使整个图形的面积被平均分成2份.在下面的图形中画出直线,并指出具体位置.
如图,由边长分别为8厘米,10厘米,12厘米的三个不同的正方形组成的图形,现请你经过C点沿一条直线把它剪开,使整个图形的面积被平均分成2份.在下面的图形中画出直线,并指出具体位置.查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| 5 |


查看答案和解析>>
科目:初中数学 来源:2011年江西省等学校招生统一考试数学卷(二) 题型:解答题
课题:探究能拼成正多边形的三角形的面积计算公式.
1.如图1,三角形的三边长分别为a、b、c,∠A=60°,现将六个这样的三角形(设面积为 )拼成一个六边形,由于大六边形三个角都是∠B+∠C=120°,所以由a边围成了一个大的正六边形,其面积可计算出为 ;由于所围成的小六边形的边长都是 ,其面积为 ,由此可得
)拼成一个六边形,由于大六边形三个角都是∠B+∠C=120°,所以由a边围成了一个大的正六边形,其面积可计算出为 ;由于所围成的小六边形的边长都是 ,其面积为 ,由此可得 =
.
=
.
2.如图2, 三角形的三边长分别为a、b、c,∠A=120°,试用这样的三角形拼成一个正三角形(设面积为 ),先画出这个正三角形,再推出
),先画出这个正三角形,再推出 的计算公式;
的计算公式;
3.推广:
对于三角形的三边长分别为a、b、c,当∠A取什么值时,能拼成一个任意正 边形吗?如果能,试写出∠A和三角形的面积
边形吗?如果能,试写出∠A和三角形的面积 的表达式;如果不能,请简要说明理由.
的表达式;如果不能,请简要说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com