
【题目】如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y=![]() 的图像经过B、C两点.
的图像经过B、C两点.

(1)求该二次函数的解析式;
(2)结合函数的图像探索:当y>0时x的取值范围.
 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 分别为数轴上的两点,
分别为数轴上的两点,![]() 点对应的数为
点对应的数为![]() ,
,![]() 点对应的数为
点对应的数为![]() .
.
![]()
(1)请写出与![]() 、
、![]() 两点距离相等的点
两点距离相等的点![]() 所对应的数;
所对应的数;
(2)现有一只电子蚂蚁![]() 从
从![]() 点出发,以
点出发,以![]() 单位/秒的速度向左运动,同时另一只电子蚂蚁
单位/秒的速度向左运动,同时另一只电子蚂蚁![]() 恰好从
恰好从![]() 点出发,以
点出发,以![]() 单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的
单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的![]() 点相遇,你知道
点相遇,你知道![]() 点对应的数是多少吗?(写出计算过程)
点对应的数是多少吗?(写出计算过程)
(3)在题(2)中,若运动t秒钟时,两只蚂蚁的距离为10,求出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
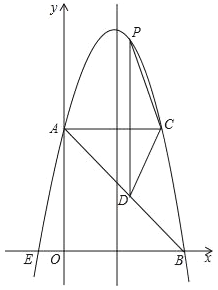
【题目】如图,在平面直角坐标系中,抛物线y=ax2+4x+c与y轴交于点A(0,5),与x轴交于点E,B,点B坐标为(5,0).
(1)求二次函数解析式及顶点坐标;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题:
(1) 18+(-12)+(-21)+(+12)
(2)8+(-10)+(-2)-(-5)
(3)![]()
(4)![]()
(5)![]()
(6)(- 1![]() )-(+6
)-(+6![]() )-2.25+
)-2.25+![]()
(7)(-![]() )×
)× ![]() ×(-
×(-![]() )
)
(8)(+![]() )×∣-
)×∣-![]() ∣×
∣×![]() ×(-
×(-![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 以上均不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红富士苹果某箱上标明苹果质量为![]() ,则这箱苹果最重为__________kg,如果某箱苹果重14.95kg,则这箱苹果_________________标准.(填“符合”或“不符合”)
,则这箱苹果最重为__________kg,如果某箱苹果重14.95kg,则这箱苹果_________________标准.(填“符合”或“不符合”)
查看答案和解析>>
科目:初中数学 来源: 题型:
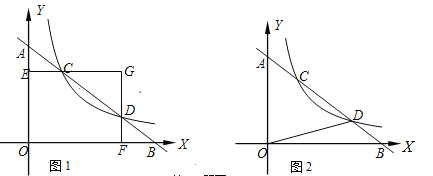
【题目】探究:如图1 ,直线l与坐标轴的正半轴分别交于A,B两点,与反比例函数![]() 的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(a,b).
的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(a,b).
(1)若![]() ,请用含n的代数式表示
,请用含n的代数式表示![]() ;
;
(2)求证: ![]() ;
;
应用:如图2,直线l与坐标轴的正半轴分别交于点A,B两点,与反比例函数![]() 的图象交于点C,D两点(点C在点D的左边),已知
的图象交于点C,D两点(点C在点D的左边),已知![]() ,△OBD的面积为1,试用含m的代数式表示k.
,△OBD的面积为1,试用含m的代数式表示k.
查看答案和解析>>
科目:初中数学 来源: 题型:
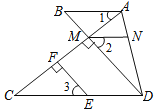
【题目】如图,已知:EF⊥AC,垂足为点F,DM⊥AC,垂足为点M,DM的延长线交AB于点B,且∠1=∠C,点N在AD上,且∠2=∠3,试说明AB∥MN.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com