
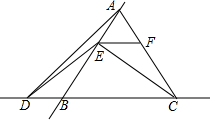
 已知:△ABC是正三角形,且边长为1,点E是直线AB上的一个动点,过点E作BC的平行线交直线AC于点F,将线段EC绕点E旋转,使点C落在直线BC上的点D处;
已知:△ABC是正三角形,且边长为1,点E是直线AB上的一个动点,过点E作BC的平行线交直线AC于点F,将线段EC绕点E旋转,使点C落在直线BC上的点D处;分析 (1)①有两种方法,易证明△AEF是正三角形,则AE=AF=EF,再证明△EDB≌△CEF,从而得出AE=BD;
②过点E作EH⊥DC于点H,设AE=x,则得出s与x的函数关系式,根据顶点坐标,得出当x=$\frac{1}{4}$时,S有最大值,求得BE,根据三角函数的定义即可得出∠ECB的正切值;
(2)当点E在BA延长线上,且AE<1时;当点E在BA延长线上,且AE>1时;当点E在AB延长线上时.共三种情况,当点E不在边AB上时,由A、D、E、C四点围成的四边面积能为$\frac{{15\sqrt{3}}}{2}$,设AE=x,分以下三种情况讨论:第一种情况:当点E在BA延长线上,且AE<1时;由(1)第①同理可得AE=BD,S四边形ADCE=S△BCE-S△BDA;第二种情况:当点E在BA延长线上,且AE>1时,S四边形AEDC=S△BDE-S△BAC;第三种情况:当点E在AB延长线上时,S四边形ADECC=S△ADC+S△EDC;
根据以上三种情况可得出当AE=$\frac{{-1+5\sqrt{5}}}{2}$或5时,由A、D、E、C四点围成的四边面积为$\frac{{15\sqrt{3}}}{2}$.
解答  解:方法一:如图在正ABC中,∠ABC=∠ACB=∠BAC=60°,AB=BC=AC,
解:方法一:如图在正ABC中,∠ABC=∠ACB=∠BAC=60°,AB=BC=AC,
∵EF∥BC,
∴∠AEF=∠AFE=60°=∠BAC,
∴△AEF是正三角形,
∴AE=AF=EF,
∴AB-AE=AC-AF,即BE=CF,
又∵∠ABC=∠EDB+∠BED═60°,
∠ACB=∠ECB+∠FCE═60°,
∵ED=EC,
∴∠EDB=∠ECB,
∴∠BED=∠FCE,
∴△EDB≌△CEF,
DB=EF,
∴AE=BD;
方法二::如图,在正ABC中,∠ABC=∠ACB=60°∠ABD=120°,
又∵∠ABC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,
∵ED=EC,
∴∠EDB=∠ECB,
∴∠BED=∠FCE,
∵EF∥BC,
∴∠AEF=∠AFE=60°=∠BAC,
∴△AEF是正三角形,∠EFC=180°-∠ACB=120°,
∴△EDB≌△CEF,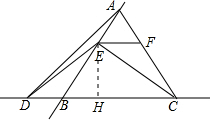
DB=EF,
∴AE=BD,
②过点E作EH⊥DC于点H,
设AE=x,则s=$\frac{1}{2}$(EF+DC)×EH=$\frac{1}{2}$(x+x+1)×$\frac{{\sqrt{3}}}{2}$(1-x),
=-$\frac{{\sqrt{3}}}{2}$x2+$\frac{{\sqrt{3}}}{4}$x+$\frac{{\sqrt{3}}}{4}$
当x=$\frac{1}{4}$时,有最大值;
此时,EB=$\frac{3}{4}$,则EH=$\frac{{3\sqrt{3}}}{8}$,BH=$\frac{3}{8}$,CH=$\frac{5}{8}$,
tan∠ECB=$\frac{EH}{CH}$=$\frac{{\frac{{3\sqrt{3}}}{8}}}{{\frac{5}{8}}}$=$\frac{{3\sqrt{3}}}{5}$,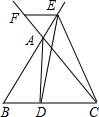
(2)当点E在BA延长线上,且AE<1时;当点E在BA延长线上,且AE>1时;当点E在AB延长线上时.共三种情况.
当点E不在边AB上时,由A、D、E、C四点围成的四边面积能为$\frac{{15\sqrt{3}}}{2}$,具体解答过程如下:
设AE=x,分以下三种情况讨论: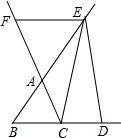
第一种情况:当点E在BA延长线上,且AE<1时;由(1)第①同理可得AE=BD,
S四边形ADCE=S△BCE-S△BDA
=$\frac{1}{2}$×BE×BC×sin60°-$\frac{1}{2}$×BE×BC×sin60°
=$\frac{1}{2}$×(x+1)×1×sin60°-$\frac{1}{2}$x×1×sin60°
=$\frac{{\sqrt{3}}}{4}$≠$\frac{{15\sqrt{3}}}{2}$,不成立;
第二种情况:当点E在BA延长线上,且AE>1时;
S四边形AEDC=S△BDE-S△BAC
=$\frac{1}{2}$×BE×BD×sin60°-$\frac{1}{2}$×BA×BC×sin60°
=$\frac{1}{2}$×(x+1)×x×sin60°-$\frac{1}{2}$×1×1×sin60°
=$\frac{{\sqrt{3}}}{4}$(x2+x-1);
由题意得:$\frac{{\sqrt{3}}}{4}$(x2+x-1)=$\frac{{15\sqrt{3}}}{2}$
解得:x1=$\frac{{-1+5\sqrt{5}}}{2}$,x1=$\frac{{-1-5\sqrt{5}}}{2}$(舍去);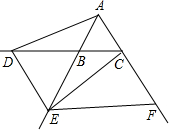
第三种情况:当点E在AB延长线上时;
S四边形ADECC=S△ADC+S△EDC
=$\frac{1}{2}$×DC×AM+$\frac{1}{2}$×DC×EN
=$\frac{1}{2}$DC×AE×sin60°
=$\frac{1}{2}$×(x+1)×x×sin60°
=$\frac{{\sqrt{3}}}{4}$(x2+x),
得:$\frac{{\sqrt{3}}}{4}$(x2+x)=$\frac{{15\sqrt{3}}}{2}$
解得:x1=5,x2=-6(舍去)
综上所述,当AE=$\frac{{-1+5\sqrt{5}}}{2}$或5时,由A、D、E、C四点围成的四边面积为$\frac{{15\sqrt{3}}}{2}$.
点评 本题考查了几何变换综合题,涉及的知识点等边三角形的判定、全等三角形的判定、二次函数的最值问题和三角函数的定义,综合性强,难度较大,解答时,需要学生具有综合运用知识的能力.


科目:初中数学 来源: 题型:选择题
| A. | 如果两个角相等,则它们是对顶角 | |
| B. | 实数包括有理数、无理数 | |
| C. | 两直线被第三直线所截,内错角相等 | |
| D. | 若a2=b2,则a=b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
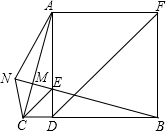 如图,已知正方形ADBF,点E在AD上,且∠AEB=105°,EC∥DF交BD的延长线于C,N为BE延长线上一点,BN交AC于M,且CE=2MN,连结AN、CN,下列结论:
如图,已知正方形ADBF,点E在AD上,且∠AEB=105°,EC∥DF交BD的延长线于C,N为BE延长线上一点,BN交AC于M,且CE=2MN,连结AN、CN,下列结论:| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①③ | B. | ①②③ | C. | ①②④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1,2 ) | B. | (-2,2) | C. | (3,-1) | D. | (3,-2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com