
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与y轴交于点A,
的图象与y轴交于点A,
与x轴交于点B,与反比例函数![]() 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
标为2,
(1)求一次函数和反比例函数的解析式;
(2)直接写出![]() 时x的取值范围.
时x的取值范围.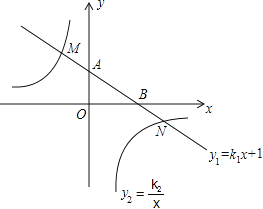
【答案】(1)y1=![]() x+1,
x+1,![]() (2)x<-2或0<x<4
(2)x<-2或0<x<4
【解析】
解:(1)∵一次函数![]() 的图象与y轴交于点A,与x轴交于点B,
的图象与y轴交于点A,与x轴交于点B,
∴A(0,1),B(![]() ,0).
,0).
∵△AOB的面积为1,∴![]() ×OB×OA=1,即
×OB×OA=1,即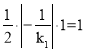 .∴
.∴![]() .
.
∴一次函数的解析式为y1=![]() x+1.
x+1.
∵点M在直线y1上,∴当y=2时,![]() x+1=2,解得x=-2.∴M的坐标为(-2,2)
x+1=2,解得x=-2.∴M的坐标为(-2,2)
又∵点M在反比例函数的图象上,∴k2=-2×2=-4,
∴反比例函数的解析式为![]() .
.
(2)当y1>y2时,x<-2或0<x<4.
(1)先由一次函数的解析式求出点A与点B的坐标,再根据△AOB的面积为1,可得到k1的值,
从而求出一次函数的解析式;得到点M的坐标,然后运用待定系数法即可求出反比例函数的解析式.
(2)y1>y2即一次函数值大于反比例函数值,只需观察一次函数的图象落在反比例函数的图象的
上方时自变量的取值范围即可,为此,先求出它们的交点坐标,再根据函数图象,可知在在点M的左边以及原点和点N之间的区间,y1>y2:
解方程组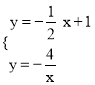 得
得![]() 或
或![]() ,
,
∴当y1>y2时,x<-2或0<x<4.


科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE.对于下列结论:①AD=DC;②△CBA∽△CDE;③![]() =
=![]() ;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )
;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )

A. ①② B. ①②③ C. ①④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=![]() (x>0)的图象上,顶点B在函数y2=
(x>0)的图象上,顶点B在函数y2=![]() (x>0)的图象上,∠ABO=30°,则
(x>0)的图象上,∠ABO=30°,则![]() = .
= .

查看答案和解析>>
科目:初中数学 来源: 题型:
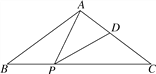
【题目】如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)求证:AC·CD=CP·BP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,AB=4,且∠ABC=∠ABE=60°,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则AM+BM+CM的最小值为_____.
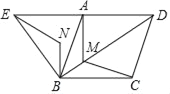
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,横坐标为a的点A在反比例函数y1═![]() (x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(1)设a=2,点B(4,2)在函数y1、y2的图象上.
①分别求函数y1、y2的表达式;
②直接写出使y1>y2>0成立的x的范围;
(2)如图①,设函数y1、y2的图象相交于点B,点B的横坐标为3a,△AA'B的面积为16,求k的值;
(3)设m=![]() ,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
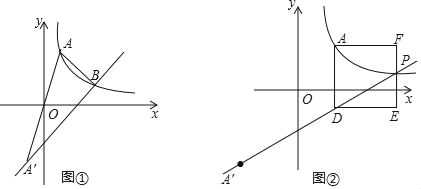
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAB的顶点坐标分别为O(0,0)、A(3,2)、B(2,0),将这三个顶点的坐标同时扩大到原来的2倍,得到对应点D、E、F.
(1)在图中画出△DEF;
(2)点E是否在直线OA上?为什么?
(3)△OAB与△DEF______位似图形(填“是”或“不是”)
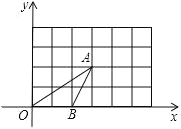
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com