
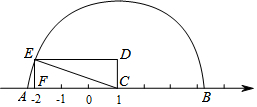
 如图所示,数轴上点C表示的数是1,点F表示的数是-2,CD=1,以CD,CF为边作长方形CDEF,以C为圆心、CE的长为半径画弧交数轴于A、B两点,则点A表示的数是1-$\sqrt{10}$,点B表示的数是1+$\sqrt{10}$.
如图所示,数轴上点C表示的数是1,点F表示的数是-2,CD=1,以CD,CF为边作长方形CDEF,以C为圆心、CE的长为半径画弧交数轴于A、B两点,则点A表示的数是1-$\sqrt{10}$,点B表示的数是1+$\sqrt{10}$. 分析 首先利用勾股定理计算出CE的长,再根据题意可得CA=CB,求出OA和OB的长即可.
解答 解:∵点C表示的数是1,点F表示的数是-2,
∴CF=3,
∵四边形CDEF是长方形,
∴EF=CD=1,∠CFE=90°,
∴CE=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
∵以C为圆心、CE长为半径画弧,
∴CA=CB,
设原点为O,则OA=$\sqrt{10}$-1,OB=$\sqrt{10}$+1,
∴点A表示的数是 1-$\sqrt{10}$,
点B表示的数是1+$\sqrt{10}$;
故答案为:1-$\sqrt{10}$;1+$\sqrt{10}$.
点评 此题主要考查了勾股定理,以及实数与数轴,关键是掌握勾股定理,计算出CE的长.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:选择题
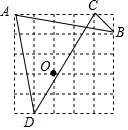 如图为5×5的网格图,A,B,C,D,O均在格点上,则点O是( )
如图为5×5的网格图,A,B,C,D,O均在格点上,则点O是( )| A. | △ACD的外心 | B. | △ABC的外心 | C. | △ACD的内心 | D. | △ABC的内心 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
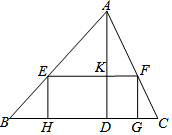 如图,已知锐角△ABC中,边BC长为12,高AD长为8.矩形EFGH的边GH在BC边长,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K.
如图,已知锐角△ABC中,边BC长为12,高AD长为8.矩形EFGH的边GH在BC边长,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,O对应的有序数对为(1,3)有一个英文单词的字母顺序对应如图中的有序数对分别为(1,2),(5,1),(5,2),(5,2),(1,3),请你把这个英文单词写出来或者翻译成中文为HELLO.
如图,O对应的有序数对为(1,3)有一个英文单词的字母顺序对应如图中的有序数对分别为(1,2),(5,1),(5,2),(5,2),(1,3),请你把这个英文单词写出来或者翻译成中文为HELLO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com