
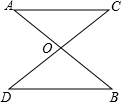
 已知,如图,AB,CD相交于0,且∠C=∠D,OC=OD,求证:△ACO≌△BDO.
已知,如图,AB,CD相交于0,且∠C=∠D,OC=OD,求证:△ACO≌△BDO.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
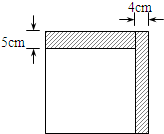 如图,小明将一张正方形的纸片减去一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,且两次剪下的两个长条的面积正好相等.求最后剩下的图形的面积.
如图,小明将一张正方形的纸片减去一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,且两次剪下的两个长条的面积正好相等.求最后剩下的图形的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +4 | +4.5 | -1 | -2.5 | -6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 下列条件中能使△ABD≌△ACD的是( )
下列条件中能使△ABD≌△ACD的是( )| A. | AB=AC,∠B=∠C | B. | AB=AC,∠ADB=∠ADC | C. | AB=AC,∠BAD=∠CAD | D. | BD=CD,∠BAD=∠CAD |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x}{10y}$ | B. | $\frac{{x}^{3}y}{10{x}^{2}{y}^{2}}$ | C. | $\frac{x}{3y}$ | D. | $\frac{{x}^{3}y}{3{x}^{2}{y}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com