
����Ŀ����ͼ������OABC�ı�OA��x���������ϣ���OC��y���������ϣ�B�������Ϊ��1��3��������O��A��BC���Ǿ���OABC��B����ʱ����ת�õ��ģ�O���ǡ����x����������ϣ�O��C�佻AB�ڵ�D��
��1�����O������꣬���жϡ�O��DB����״��Ҫ˵�����ɣ�
��2�����C��O������ֱ�ߵĽ���ʽ��
��3���ӳ�BA��MʹAM=1���ڣ�2������õ�ֱ�����Ƿ���ڵ�P��ʹ�á�POM�����߶�OMΪֱ�DZߵ�ֱ�������Σ������ڣ���ֱ��д��P������ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��ͼ������OB��O��B����OB=O��B��
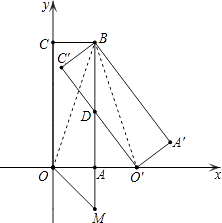
���ı���OABC�Ǿ��Σ�
��BA��OA��
��AO=AO�䣬
��B���������1��3����
��OA=1��
��AO��=1��
���O��������ǣ�2��0����
��O��DB����������
�������£��ڡ�BC��D���O��AD�У�
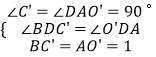 ��
��
���BC��D�ա�O��AD��AAS����
��BD=O��D��
���O��DB�ǵ���������
��2��
�⣺���D������Ϊ��1��a������AD=a��
�ߵ�B�������ǣ�1��3����
��O��D=3��a��
��Rt��ADO����AD2+AO��2=O��D2��
��a2+12=��3��a��2��
���a= ![]() ��
��
���D��������1�� ![]() ����
����
��ֱ��C��O��Ľ���ʽΪy=kx+b��
��  ��
��
��� 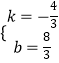 ��
��
���C��O������ֱ�ߵĽ���ʽ��y=�� ![]() x+
x+ ![]()
��3��
�⣺��AM=1��AO=1����AM��AO��
���AOM�ǵ���ֱ�������Σ�
��PM����һֱ�DZ�ʱ����PMA=45�㣬
��PA=AM=1����P���O���غϣ�
���P�������ǣ�2��0����
��PO����һֱ�DZߣ���POA=45�㣬��PO���ڵ�ֱ��Ϊy=x��
�� 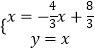 ��
��
��� ![]() ��
��
���P������ΪP��2��0���� ![]() ��
�� ![]() ����
����

����������1������OB��O��B��������ת�����ʿɵ�OB=O��B���ٸ��ݾ��ε�����BA��OA���ٸ��ݵ������������ߺ�һ�����ʿɵ�AO=AO�䣬Ȼ����ݵ�B���������AO�ij��ȣ��ٵõ�AO��ij��ȣ���O������꼴�ɵõ������ýǽDZ�֤����BC��D���O��ADȫ�ȣ�Ȼ�����ȫ�������ζ�Ӧ����ȵõ�BD=O��D�����ԡ�O��DB�ǵ��������Σ���2�����D�������ǣ�1��a������ʾ��O��D�ij��ȣ�Ȼ�����ù��ɶ�����ʽ���a��ֵ���Ӷ��õ���D�����꣬�ٸ��ݴ���ϵ������ʽ�������ֱ��C��O��Ľ���ʽ����3������AM=1�ɵá�AOM�ǵ���ֱ�������Σ�Ȼ��֢�PM����һֱ�DZߣ���PMA=45�㣬��PO����һֱ�DZߣ���POA=45�����������ʽ���м��㼴�ɵý⣮
�����㾫��������ȫ�������ε����ʺ;��ε������ǽ����ĸ�������Ҫ֪��ȫ�������εĶ�Ӧ�����; ȫ�������εĶ�Ӧ����ȣ����ε��ĸ��Ƕ���ֱ�ǣ����εĶԽ�����ȣ�


 ��ҵ����ϵ�д�
��ҵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ�������
A. 2x2x3=2x6 B. ����2a��3=��6a3 C. ��a3��2=a5 D. x3��x2=x
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֽƬABCD�۵���ʹ��D���B�غϣ���C����C�������ۺ�ΪEF����AB=1��BC=2������ABE����BC��F���ܳ�֮��Ϊ��������

A. 3 B. 4 C. 6 D. 8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��֪��ABE�ա�ACD,��AB=AC.
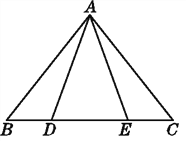
(1)˵����ABE���������ı任������ACD�غ�.
(2)��BAD���CAE�кι�ϵ?��˵������.
(3)BD��CE�����?Ϊʲô?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��D���A��0��6����B��0����4����C��x��y����ƽ���ı��ε��ĸ����㣬����x��y����x��y+3=0����CD������СֵΪ�� ��
A.![]()
B.4
C.2
D.2 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ҹ���������������������û����ͽ��������Ϊ���㣮Ϊ�˵���ѧ������������֪ʶ���˽�̶ȣ�ijУ��ѧ��������һ�γ������飬����������Ϊ�ĸ��ȼ���A���dz��˽⣻B���Ƚ��˽⣻C�������˽⣻D�����˽⣮���ݵ���ͳ�ƽ���������˲�����������ͳ��ͼ����
�������˽�̶ȵ�ͳ�Ʊ���


����ͳ��ͼ�����ش��������⣮
��1�����β�������ѧ�������� ���ˣ�m=�� ����n=�� ����
��2��ͼ2��ʾ������ͳ��ͼ��D������������Ӧ��Բ�Ľ����� ���ȣ�
��3���벹ȫͼ1ʾ��������ͳ��ͼ��
��4�����ݵ�������ѧУ����չ��������֪ʶ������ij��Ҫ�����dz��˽���̬�ȵ�С����С����ѡһ�˲μӣ��������������Ϸ��ȷ������������ǣ����ĸ���ȫ��ͬ��ƹ�����������1��2��3��4��Ȼ��ŵ�һ�������Ĵ��У�һ�����ȴӴ����������һ������һ���ٴ�ʣ�µ����������������һ�������������������ϵ����ֺ�Ϊ��������С��ȥ������С��ȥ��������״ͼ���б���˵�������Ϸ�����Ƿ�ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����1=��2����3+��4= 180����ȷ��ֱ��a��c��λ�ù�ϵ����˵�����ɣ�
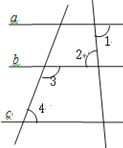
�⣺a c��
���ɣ��ߡ�1=��2�� ��,
�� a // ( )��
�� ��3+��4= 180�㣨 ��,
�� c // ( )��
�� a // ,c // ,
�� // ( )��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com