解:(1)S=-t
2+6t,0<t<6;
(2)由题意知AP=t,BQ=2t.
①若△PBQ∽△ABC,则
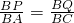
∴
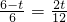
解得t=3,
②若△PBQ∽△CBA,则
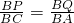
∴
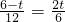
解得t=

.
即当点P移动3s或

s时,△PBQ与△ABC相似;
(3)作MD⊥AB于D,ME⊥BC于E.
∴∠ADM=90°,
又∠B=90°,
∴∠ADM=∠B,
∴DM∥BC,
∴

,
又∵M是AC的中点,
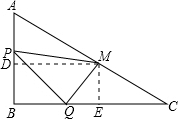
∴
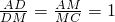
,即D是AB的中点,
∴
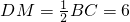
.
同理
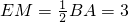
,
∵
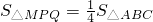
,
∴
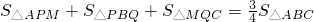
,
∴
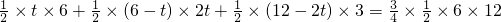
即t
2-6t+9=0.
t
1=t
2=3,
即点P移动3s时,
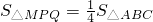
分析:(1)根据三角形面积公式,知△PBQ的面积S=

×BP×BQ.而BP=AB-AP=6-t,BQ=2t,代入即可求出S与t的函数关系式,由P点只能从A出发沿边AB向点B移动,可知t的取值范围;
(2)假设△PBQ能与△ABC相似,由于∠PBC=∠ABC=90°,则只能点B与点B对应,可分两种情况讨论:①点P与点A对应,即△PBQ∽△ABC;②点P与点C对应,即△PBQ∽△CBA.根据相似三角形的对应边成比例列出关于t的方程,从而求出t值;
(3)如果
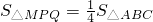
,那么
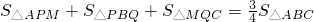
,又AP=t,BP=6-t,BQ=2t,CQ=12-2t,根据三角形的面积公式可知,只需求出△APM中AP边上的高及△MQC中CQ边上的高,即可根据等量关系列出方程,进而求出方程的解.为此,作MD⊥AB于D,ME⊥BC于E.根据中位线的判定及性质可求出DM、ME的值.
点评:本题结合三角形面积公式考查了求二次函数的解析式,结合相似三角形的判定和性质考查了路程问题,以及组合图形面积的计算.

 的取值范围为______;
的取值范围为______; ?
?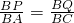
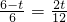
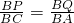
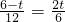
 .
. s时,△PBQ与△ABC相似;
s时,△PBQ与△ABC相似; ,
,
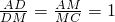 ,即D是AB的中点,
,即D是AB的中点,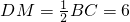 .
.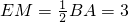 ,
,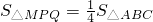 ,
,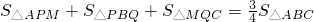 ,
,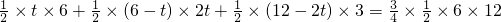
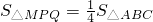
 ×BP×BQ.而BP=AB-AP=6-t,BQ=2t,代入即可求出S与t的函数关系式,由P点只能从A出发沿边AB向点B移动,可知t的取值范围;
×BP×BQ.而BP=AB-AP=6-t,BQ=2t,代入即可求出S与t的函数关系式,由P点只能从A出发沿边AB向点B移动,可知t的取值范围;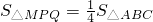 ,那么
,那么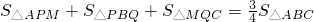 ,又AP=t,BP=6-t,BQ=2t,CQ=12-2t,根据三角形的面积公式可知,只需求出△APM中AP边上的高及△MQC中CQ边上的高,即可根据等量关系列出方程,进而求出方程的解.为此,作MD⊥AB于D,ME⊥BC于E.根据中位线的判定及性质可求出DM、ME的值.
,又AP=t,BP=6-t,BQ=2t,CQ=12-2t,根据三角形的面积公式可知,只需求出△APM中AP边上的高及△MQC中CQ边上的高,即可根据等量关系列出方程,进而求出方程的解.为此,作MD⊥AB于D,ME⊥BC于E.根据中位线的判定及性质可求出DM、ME的值.

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为