
如图,△ABC的三个顶点 都在⊙O上,AP⊥BC于P,AM为⊙O的直径.
都在⊙O上,AP⊥BC于P,AM为⊙O的直径.
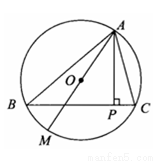
求证:∠BAM=∠CAP.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年福建省龙岩市分校九年级上学期第三次阶段考试数学试卷(解析版) 题型:填空题
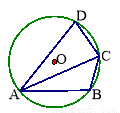
如图,在⊙O中,∠D=70°,∠ACB=50°,则∠BAC= .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市平谷区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,一次函数的图象与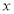 轴、
轴、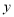 轴分别相交于A、B两点,且与反比例函数的图象在第二象限交于点C.如果点A的坐标为
轴分别相交于A、B两点,且与反比例函数的图象在第二象限交于点C.如果点A的坐标为 ,OA=2OB,点 B是AC的中点.
,OA=2OB,点 B是AC的中点.

(1)求点C的坐标;
(2)求一次函数和反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市平谷区九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,已知A、B、C三点在⊙O上,∠A=50°,则∠BOC的度数为

A.50° B.25° C.75° D.100°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市九年级上学期期中检测数学试卷(解析版) 题型:解答题
阅读下面的材料:
小明在学习中遇到这样一个问题:若1≤x≤m,求二次函数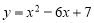 的最大值.他画图研究后发现,
的最大值.他画图研究后发现,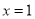 和
和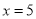 时的函数值相等,于是他认为需要对
时的函数值相等,于是他认为需要对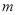 进行分类讨论.他的解答过程如下:
进行分类讨论.他的解答过程如下:

∵二次函数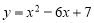 的对称轴为直线
的对称轴为直线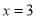 ,
,
∴由对称性可知,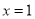 和
和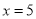 时的函数值相等.
时的函数值相等.
∴若1≤m<5,则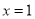 时,
时,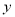 的最大值为2;
的最大值为2;
若m≥5,则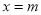 时,
时,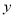 的最大值为
的最大值为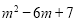 .
.
请你参考小明的思路,解答下列问题:
(1)当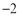 ≤x≤4时,二次函数
≤x≤4时,二次函数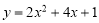 的最大值为_______;
的最大值为_______;
(2)若p≤x≤2,求二次函数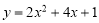 的最大值;
的最大值;
(3)若t≤x≤t+2时,二次函数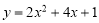 的最大值为31,则
的最大值为31,则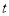 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市九年级上学期期中检测数学试卷(解析版) 题型:填空题
如图,直线l:y=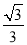 x,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y一轴于点A2;再过点A2作y轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,按此做法进行下去,点A4的坐标为(_______,_______);点An的坐标为(_______,_______).
x,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y一轴于点A2;再过点A2作y轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,按此做法进行下去,点A4的坐标为(_______,_______);点An的坐标为(_______,_______).

查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市九年级上学期期中检测数学试卷(解析版) 题型:选择题
如图,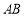 为⊙
为⊙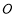 的直径,弦
的直径,弦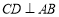 ,垂足为点
,垂足为点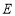 ,连结
,连结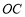 ,若
,若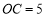 ,
,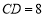 ,则
,则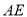 的长为( )
的长为( )
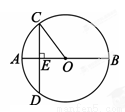
A.5 B.4 C.3 D.2
B.4 C.3 D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com