
分析 (1)根据${a}_{1}=-\frac{1}{3}$,可得${a}_{2}=\frac{1}{1-(-\frac{1}{3})}=\frac{3}{4}$,同理,求出a3,a4的值各是多少即可.
(2)首先根据a1,a2,a3,a4,a5,a6的值,可得每3个数为一个循环,然后求出每个循环三个数的和,以及循环数各是多少;最后把它们相乘,求出a1+a2+a3+…+a36的值是多少即可.
解答 解:(1)∵${a}_{1}=-\frac{1}{3}$,
∴${a}_{2}=\frac{1}{1-(-\frac{1}{3})}=\frac{3}{4}$,
a3=$\frac{1}{1-\frac{3}{4}}=4$,
a4=$\frac{1}{1-4}=-\frac{1}{3}$.
(2)∵a1=-$\frac{1}{3}$,a2=$\frac{3}{4}$,a3=4,a4=-$\frac{1}{3}$,a5=$\frac{1}{1-(-\frac{1}{3})}=\frac{3}{4}$,a6=$\frac{1}{1-\frac{3}{4}}=4$,…,
∴每3个数为一个循环,分别是-$\frac{1}{3}、\frac{3}{4}、4$,
∴a1+a2+a3+…+a36
=($-\frac{1}{3}+\frac{3}{4}+4$)×(36÷3)
=4$\frac{5}{12}×12$
=53
即a1+a2+a3+…+a36的值是53.
点评 此题主要考查了探寻数列规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:这列数中,每3个数为一个循环,分别是-$\frac{1}{3}、\frac{3}{4}、4$.


科目:初中数学 来源: 题型:填空题
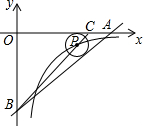 如图,OA在x轴上,OB在y轴上,OA=8,AB=10,点C在边OA上,AC=2,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过圆心P,则k=-5.
如图,OA在x轴上,OB在y轴上,OA=8,AB=10,点C在边OA上,AC=2,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过圆心P,则k=-5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
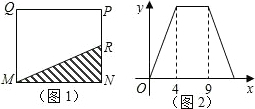 如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到( )
如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到( )| A. | M处 | B. | N处 | C. | P处 | D. | Q处 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
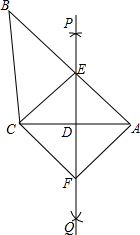 如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
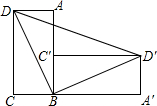 将矩形ABCD绕点B顺时针旋转90°后得到矩形A′BC′D′,若AB=12,AD=5,则△DBD′的面积为( )
将矩形ABCD绕点B顺时针旋转90°后得到矩形A′BC′D′,若AB=12,AD=5,则△DBD′的面积为( )| A. | 13 | B. | 26 | C. | 84.5 | D. | 169 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
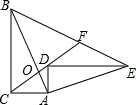 如图,在直角三角形ABC中,∠ACB=90°,点O在AB上,且CA=CO,若将直角三角形ABC绕着点A顺时针旋转,得到直角三角形AED,B、C的对应点分别为E、D,且点D落在CO的延长线上,连接BE交CO的延长线于点F,若CA=6,AB=18,则BF的长为14.
如图,在直角三角形ABC中,∠ACB=90°,点O在AB上,且CA=CO,若将直角三角形ABC绕着点A顺时针旋转,得到直角三角形AED,B、C的对应点分别为E、D,且点D落在CO的延长线上,连接BE交CO的延长线于点F,若CA=6,AB=18,则BF的长为14.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com